1. Introduction
Dielectric and ferroelectric materials have gained popularity due to their unique features and prospective uses in a variety of fields, including sensors, capacitors, data storage, and energy harvesting.1,2) Among them, BaTiO3-based ceramics have been widely studied in the past decade for the purpose to acquire high dielectric constant, strong piezoelectricity, and good thermal stability.3,4,5,6) However, to further enhance their targeted properties, doping elements with different valence states into BaTiO3 has been proved to be an effective and practicable way.7,8,9) In particular, the B-site doping with quadrivalent and/or trivalent elements has been reported to have a significant impact on the dielectric and piezoelectric properties of BaTiO3-based ceramics because of the known localized lattice defect states.10)
According to a literature conducted by Lee et al.,11) it was observed that with the increase of doping concentration of Al, the Curie point of Ba(Ti1-xAlx)O3 showed a downward shift to lower temperatures, and the dielectric constants exhibited a reduction at low frequencies. Cao et al.12) reported the dielectric behavior of Nb-doped Ba(ZrxTi1-x)O3 ceramics, and effect of the variation of Nb2O5 content and sintering temperature on the dielectric constant was explained. A recent literature reported the dielectric properties of Fe-doped BaTi0.8Sn0.2O3 ceramics, and the defect dipoles and nano-polar regions originated from the coexistence of Fe2+ and Fe3+ were shown to influence the permittivity, the Curie temperature and the dielectric tenability.13)
In most cases, the valence state of Al is +3, while that of Nb is +5. The chemical state of the Ti ions in BaTiO3 is +4. Substituting for Ti on the B-site with Al and Nb ions is expected to develop high performance of dielectric properties and elicit relaxation phenomena of BaTiO3-based ceramics due to the presence of localized defect dipoles. In this work, Ba(Al0.5Nb0.5)xTi1-xO3 ceramics with x = 0, 0.04, 0.06, and 0.08 were synthesized via a standard high-temperature solid-state reaction method. The dielectric and electric modulus characteristics of the prepared specimens were investigated. The purpose of this study is to evaluate the possibility of (Al, Nb) co-doping to modify the properties of BaTiO3 ceramics and to determine the optimal doping concentration to achieve a high dielectric constant and low dielectric loss, which can carry significant implications for their prospective utilization in piezoelectric and energy storage devices.
2. Experimental Procedure
The ceramic Ba(Al0.5Nb0.5)xTi1-xO3 (BANT) samples were synthesized by employing titanium dioxide (TiO2), barium carbonate (BaCO3), aluminum oxide (Al2O3), and niobium pentoxide (Nb2O5) as the precursor ingredients. Four samples were created by assigning x values to x = 0, 0.04, 0.06, and 0.08, specifically, and the corresponding samples were labeled as BANT00, BANT04, BANT06, and BANT08, respectively. The stoichiometric powders were measured using an electronic precision balance and thoroughly blended and milled to create a homogeneous mixture. This combination was then transferred into an alumina crucible and subjected to a Muffle furnace pre-sintering at a temperature of 1,250 °C for 4 h, resulting in the synthesis of BANT powders. The ground powders were inserted into a cylindrical matrix and subjected to uniaxial pressing at a pressure of 14 MPa. This process resulted in the formation of 10-diameter pellets with a thickness of 3 mm. Subsequently, these pellets were sintered at a temperature of 1,300 °C for 10 h, leading to the formation of BANT ceramic samples. The relative bulk density of the prepared samples was measured to be about 95 % by Archimedes method.
The samples’ crystal structure was examined using an X-ray diffractometer (XRD, Bruker D8-A25). The morphology of the sintered ceramic samples was studied by a field emission scanning electron microscope (SEM, Model SU8600, Hitachi Co.). A source of Mg-Kα radiation was employed in X-ray photoelectron spectroscopy (XPS, VGESCALab-5) to investigate the chemical states of the components. The dielectric properties were studied using a QuadTech 1730 LCR digital bridge within a frequency range of 40 Hz to 1.1 MHz. The electric modulus spectrum was recorded using an HP4194A analyzer. The data were collected in the temperature range of 100~380 K.
3. Results and Discussion
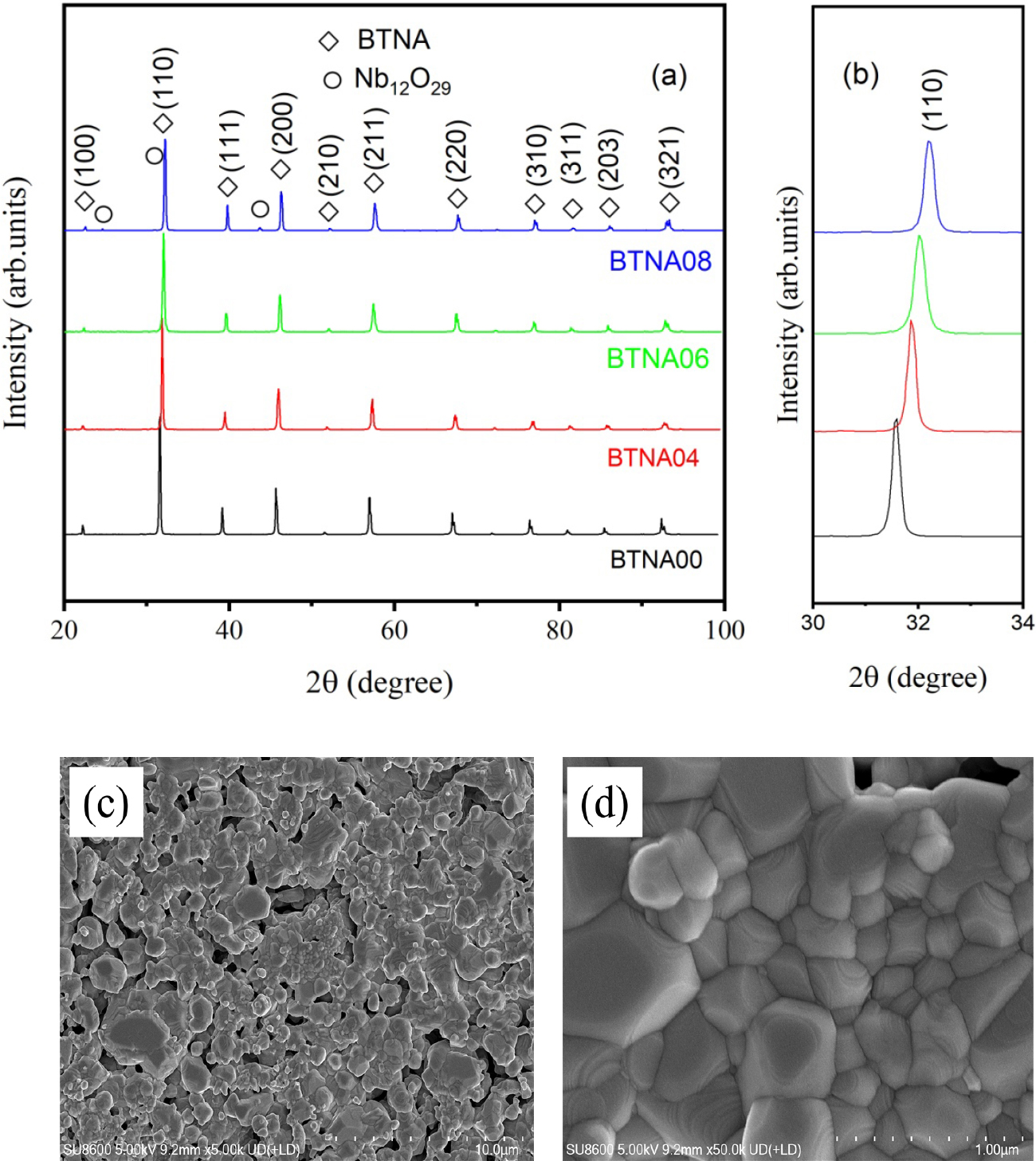
Fig. 1 shows the XRD patterns of the prepared samples. The peaks marked with diamonds are related to the tetragonal perovskite phase matched well with the PDF Card No. 05-0626. The results indicate that a small amount of Al+Nb co-doping into BaTiO3 does not change the crystal structure significantly. As the doping concentration increases to x = 0.08, weak secondary phases marked with circles for BANT08 are related to polycrystalline structure of Nb12O29 matched well with the PDF Card No. 34-1169. Fig. 1(b) shows the location of the strongest diffraction peaks of the samples. It is clear that when doping concentration increases, the peak shifts slightly in the direction of the high angle, indicating a reduction in the lattice parameters. In the case of tetragonal phase, the relationship between the X-ray Bragg diffraction angle θ and the Miller indices (hkl) of the lattice planes can be expressed as Eq. (1).
where, λ = 1.54Å. By using the positions of diffraction peaks, the lattice parameters and can be calculated. The determined lattice constants for the samples are listed in Table 1. As is known, there is little difference between the size of Ti4+ (~61 pm) and Nb5+ (~63 pm), while the radius of Al3+ ion is about 53.5 pm. It is doping with smaller ions that causes the lattice constant to drop.
Table 1.
Lattice parameters of the prepared samples.
| Sample | a (Å) | c (Å) |
| BANT00 | 3.990 | 4.040 |
| BANT04 | 3.977 | 4.026 |
| BANT06 | 3.969 | 4.001 |
| BANT08 | 3.952 | 3.993 |
Typical SEM images of BANT04 are shown in Fig. 1(c, d). It reveals the distribution of grain and grain boundary in our samples, and the mean grain size is about 0.1~0.4 µm. It should be noted that the doping ions have on obvious effect on the average grain size, which is consistent with the literature.14,15)
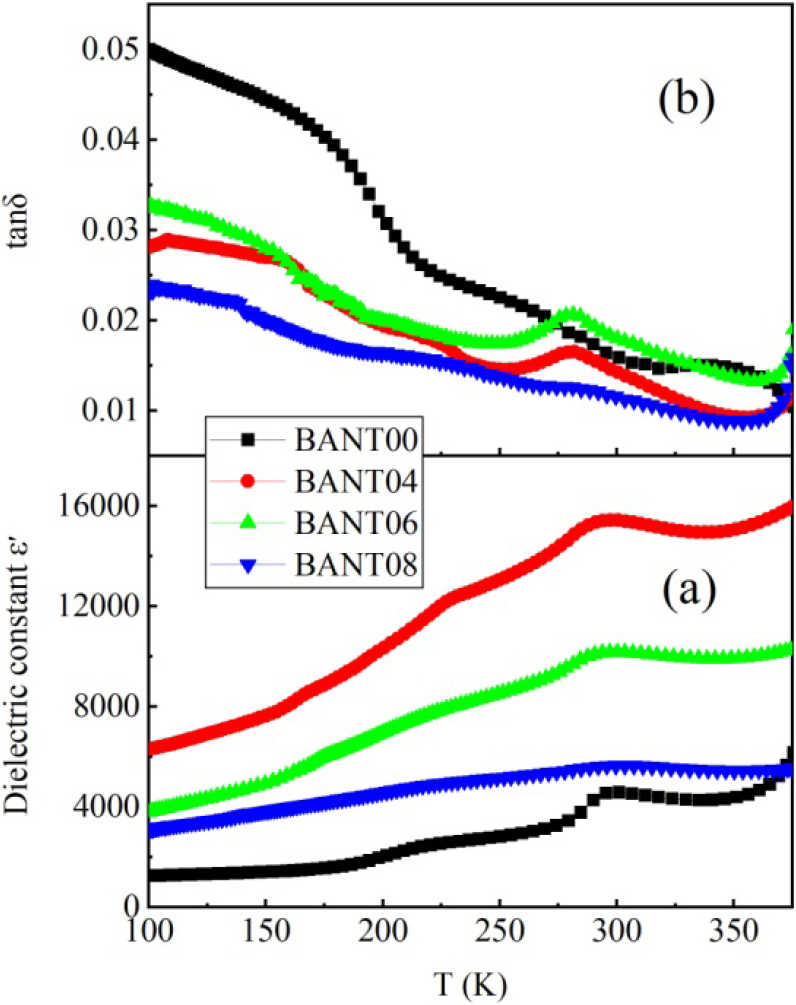
Fig. 2 illustrates the variation of the dielectric constant ε′ and the loss tangent tanδ of the prepared samples as a function of temperature at 1 kHz. The maximum value of ε′ exceeds 15,000, and the minimum value of tanδ is lower than 0.01 when the doping concentration is 4 %. It is obvious that Al+Nb co-doping contributes to the increase of dielectric constant [Fig. 2(a)] and the reduction of dielectric loss [Fig. 2(b)]. As for BANT00, the peak around 280 K in Fig. 2(a) corresponds to the ferroelectric-ferroelectric phase transition of BaTiO3 materials. With the increase of the doping concentration, the phase transition shifts to a lower temperature [as shown in Fig. 2(b)]. This result is similar to that of the previous reports on the B-site doping of BaTiO3 materials.16,17) When the doping concentration increases to 8 %, the dielectric peak decreases and broadens. This is due to the fact that excessive Nb or Al dopants are located in the grain boundary region, resulting in a reduction in grain size and flattening the curves of BANT08.
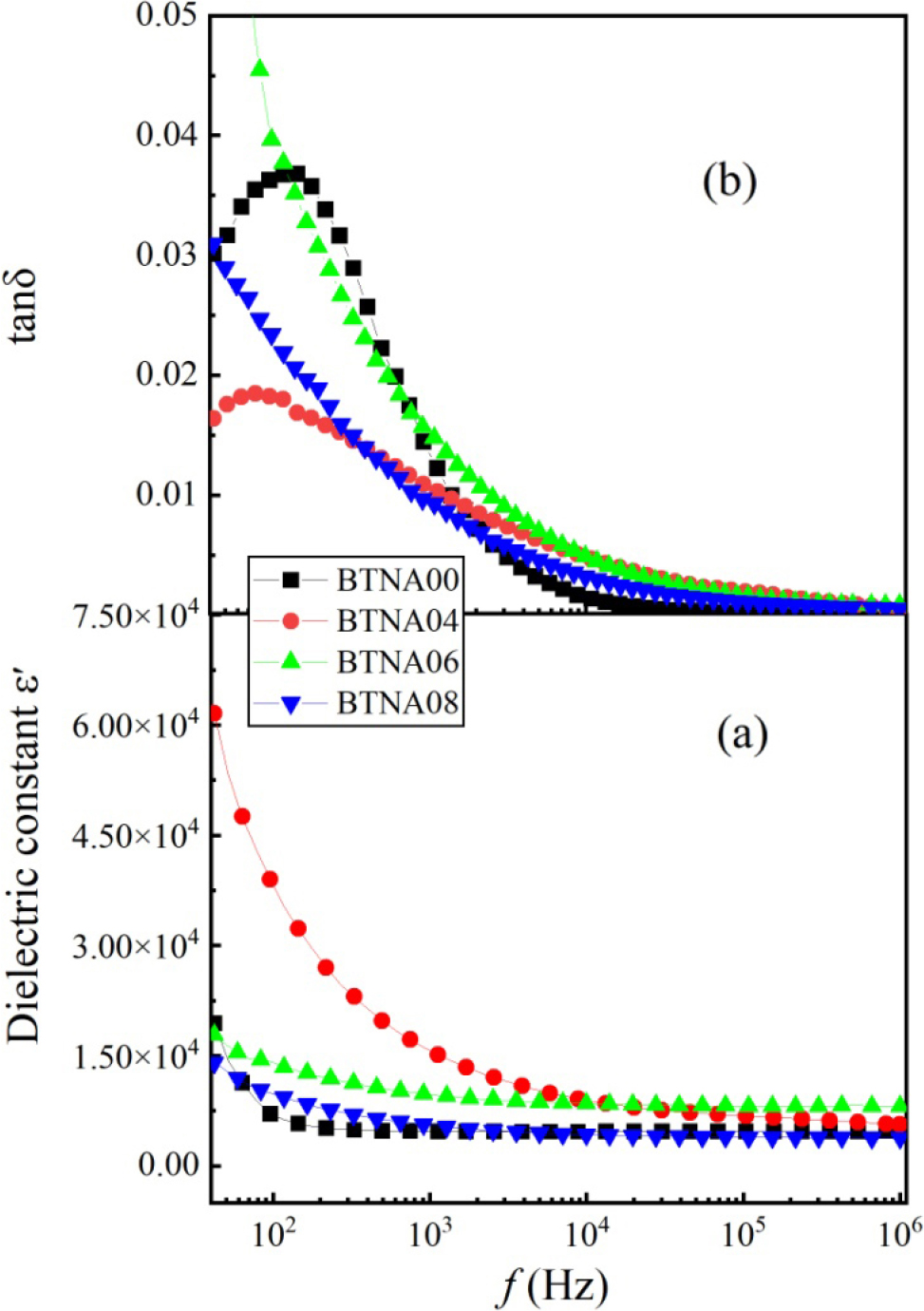
Fig. 3(a, b) show the frequency dependence of ε′ and tanδ of BANT ceramic samples at room temperature, respectively. The weak frequency dependency of the dielectric constant can be seen in the doped samples, with the exception of BANT04, and the values tend to be stable when the frequency exceeds 10 kHz, which was caused by the weak electron polarization at high frequency.18,19) The dielectric loss decreases with the increase of doping concentration in the low-frequency scope. The sample BANT04 has a higher dielectric constant and lower loss, which can be explained by the fact that the relaxation phenomenon at low frequencies could have led to a change in the electric dipole moment inside the material, resulting in a sharp increase in the dielectric constant of the sample at low frequencies. The relaxation peak of BANT04 seems to be located at lower frequency, but it is not fully displayed due to the measurement range.
In general, the observed exponential decrease in dielectric loss suggests a correlation between relaxation phenomena and the movement of carrier ions, as well as the corresponding relaxation of neighbouring ions. The behavior that was observed can be characterized using a universal dielectric response (UDR) model by Eqs. (2) and (3), as mentioned in reference.20)
where, ε∞ represents the high-frequency value of ε′(f), ε0 denotes the electric permittivity of free space, while and are constants.
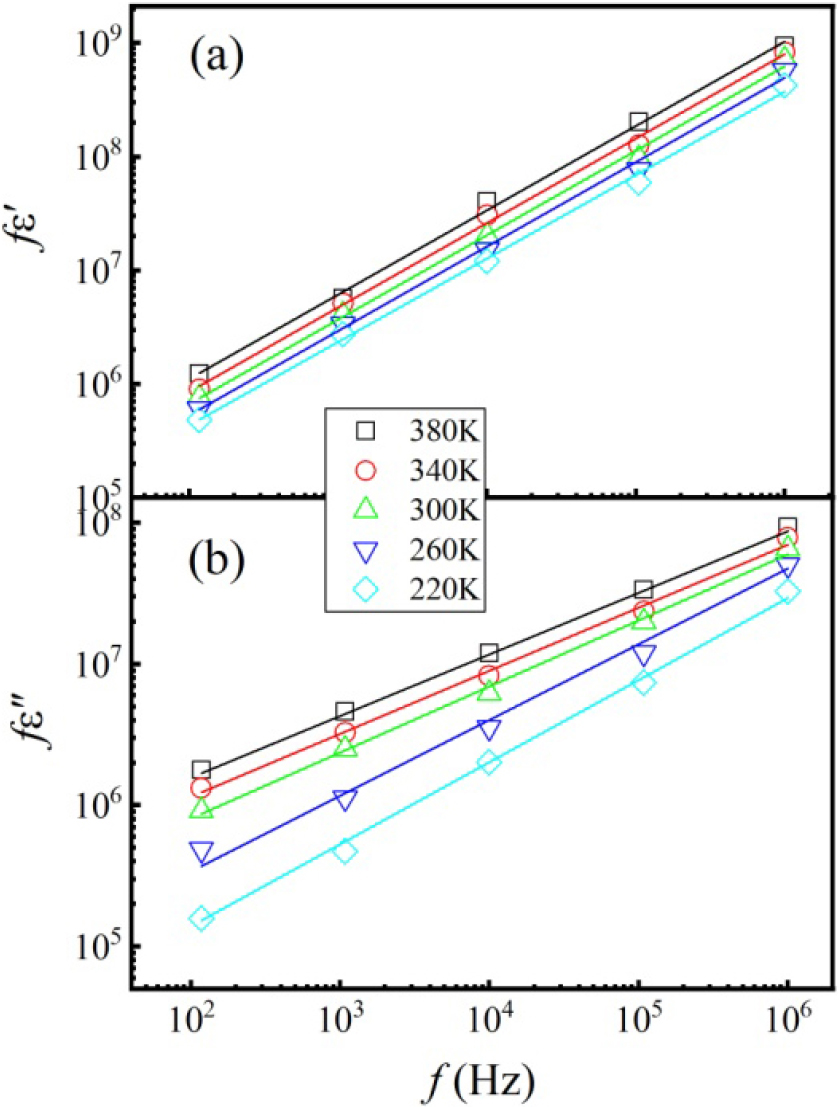
According to the Eqs. (2) and (3), it is expected that a linear relationship with a slope denoted as will be observed when plotting log fε′ against log f, as well as log fε″ against log f, at a specific temperature. The relationship is confirmed in Fig. 4 by a log-log graph for the sample BANT04 in the temperature range of 220~380 K. Through the linear fitting, the plot of log fε′~log f in Fig. 4(a) yields a value of about 0.80. Similarly, the plot of log fε″ vs log f in Fig. 4(b) provides a value of about 0.30~ 0.56. The obtained values of are consistent with the UDR model.21) Similar results are obtained for the other samples. The parameter provides insights into the polarizability, complexity, and frequency response characteristics of these perovskite dielectric materials, which can help us understand dielectric characteristics exhibited by these materials and establish a theoretical framework to support their practical utilization.
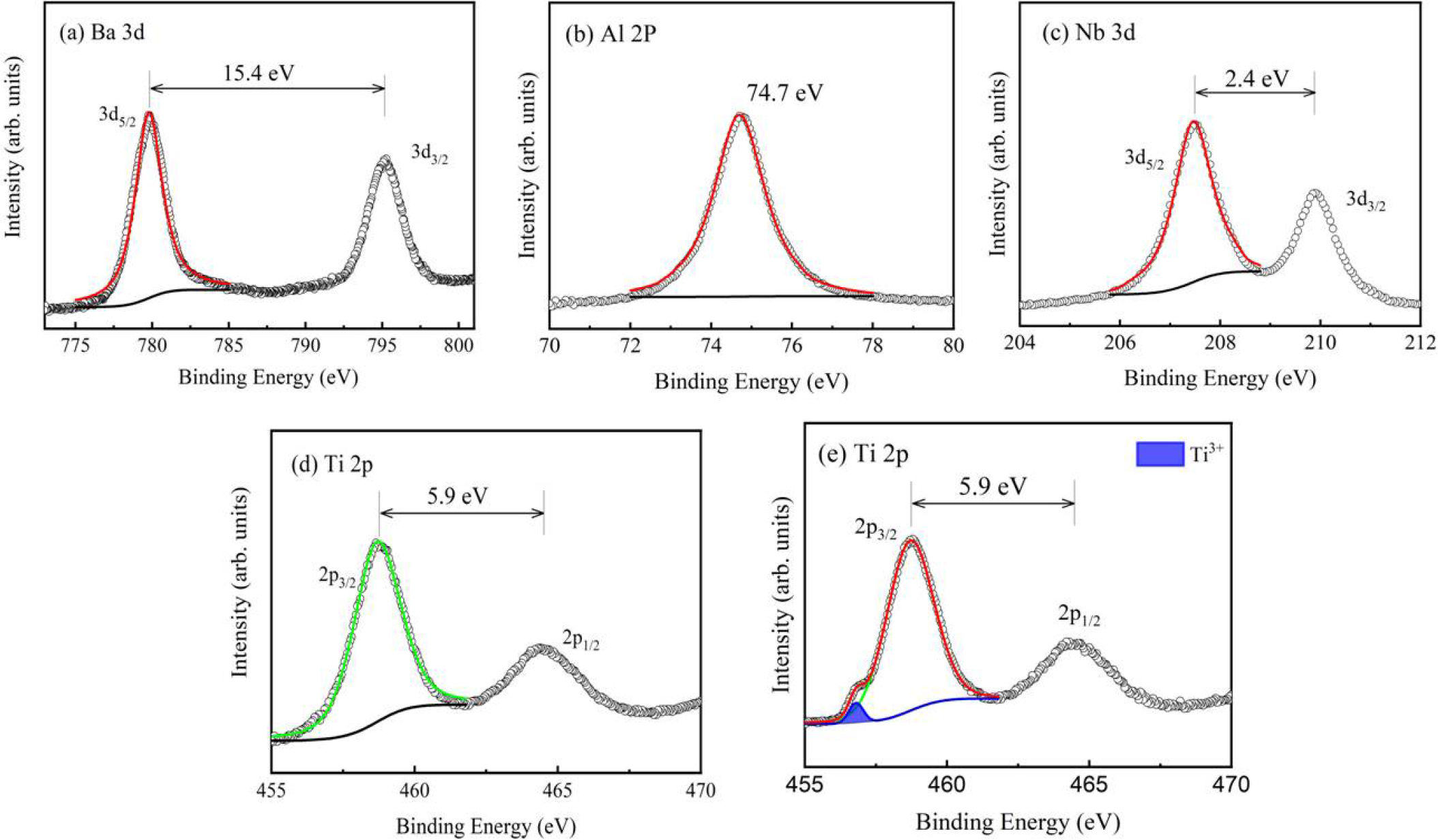
It is believed that the observed dielectric properties of the prepare BANT samples are closely related to the chemical environment of the components. XPS data were recorded to illustrate the chemical state of the elements for the BANT samples. Typical results for BANT04 are shown in Fig. 5(a-c). The Ba 3d5/2 and 3d3/2 peaks [Fig. 5(a)] are observed at 779.8 and 795.2 eV, respectively, revealing the presence of Ba2+. The Al 2p peak [Fig. 5(b)] at 74.7 eV has closely-spaced spin-orbit components, which can be ignored for Al3+. The values of 207.4 eV (Nb 3d5/2) and 209.8 eV (Nb 3d3/2) [Fig. 5(c)] manifest the chemical state of Nb5+. All the samples show roughly the same spectra for Ba 3d, Al 2p, and Nb 3d, which suggest the identical chemical state of these three component elements in the BANT samples. The Ti 2p3/2 and 2p1/2 peaks for BANT00 [Fig. 5(d)] locate at 458.7 and 464.6 eV, respectively, indicating the existence of Ti4+. With the increase of doping concentration, however, low-energy shoulder located at 456.8 eV appears which gives the existence of Ti3+ ions, as shown in Fig. 5(e).
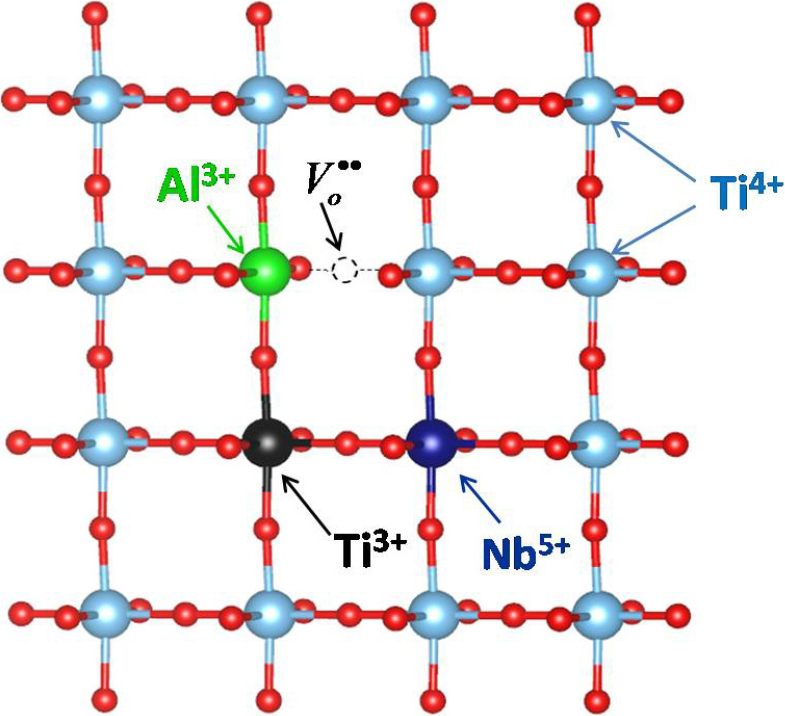
During the solid-state reaction, the cations Al3+ and Nb5+ were incorporated into the B-site of BaTiO3. When Al is substituted for the B-site Ti, it can lead to the formation of a negatively charged ionic defect []. In order to compensate for this acceptor-type defect center, an oxygen defect [] is created. This process can be expressed by Eq. (4).
In much the same way, when Nb is substituted for the Ti, it can lead to the formation of a positively charged ionic defect []. In order to compensate for this donor-type defect center [], Ti4+ is reduced to Ti3+. The mechanisms can be expressed as Eq. (5).
By using a ball-and-stick illustration, the sketch of the Ti(Al,Nb)-O structure is shown in Fig. 6. The defect complexes [], and [] can be seen clearly. The defects [] can capture the electrons from the surrounding oxygen vacancies. At the same time, the extra electrons from [] hop between the Ti3+ and Ti4+ ions. The electron-pinned defect-dipoles arise as the electrons are localized, which contributes to the observed colossal dielectric permittivity.22)
The phenomena of polarization and dielectric relaxation have a strong correlation with the process of charge transfer. The electrical properties of the internal grains in ceramics exhibit distinct variations when compared to the electrical characteristics observed at the grain borders. Hence, it is imperative to perform an exclusive examination of the internal grains and grain boundaries in order to comprehend the underlying processes of polarization and dielectric relaxation. The electrical characteristics of a ceramic material composed of grains and grain boundaries can be commonly modeled using a series-equivalent circuit with two RC elements.23) The complex electric modulus in this particular case can be expressed through the Eqs. (6), (7), (8).24)
where, Rg, Rgb, Cg, and Cg, are the resistance and capacitance associated with grain and grain boundaries, respectively, and C0 represents the capacitance of a vacuum, and ω = 2πf is the angular frequency. At high-frequency limit, Eq. (7) can be reformulated as Eq. (9).
As is known, the electrical resistance and capacitance of grains are significantly lower compared with that of grain boundaries. Thus, the expression M′ can be expressed approximately as C0/Cg, indicating that the real component of the modulus in the high frequency region is in inverse ratio to the value of the grain capacitance.
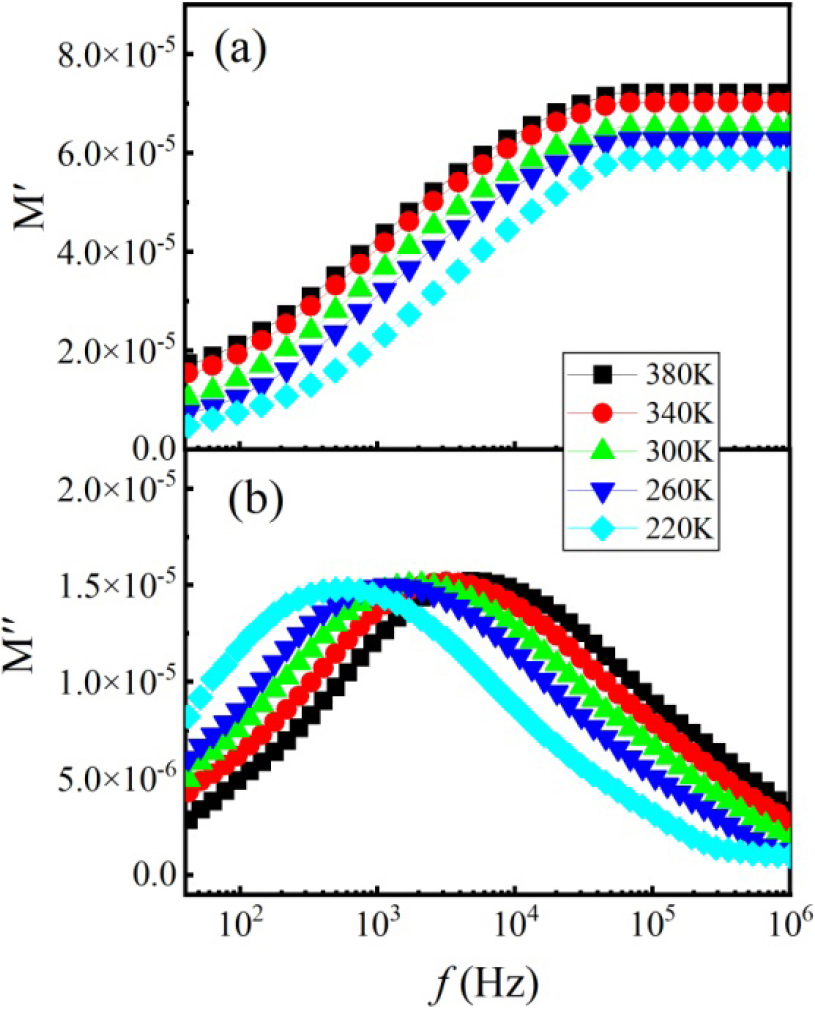
Fig. 7(a, b) show the frequency dependence of M′ and M″ for BANT04 at some different temperatures, respectively. It is obvious that the M′ plateau in the higher-frequency range increases with temperature increasing. This change indicates the decrease of the capacitance of the grains, as suggested by Eq. (8). This phenomenon clearly exhibits a quasi-electric dipoles characteristic. This quasi-electric behavior in the high frequency range demonstrates inherent properties within the sample grains, which can be attributed to the influence of ion displacement polarization in the BANT lattice. These results were consistent with the research in Fe-substituted CaCu3Ti4O12 ceramics25) and Ca+Sr substituted BaTiO3 ceramics.26) It can be seen that the donor and acceptor co-doping contributes to the temperature and frequency stability of the energy storage properties and the pulsed discharging performance of BaTiO3-based materials, which paved the way of corresponding products into practical application in high-power capacitors.27,28)
The peaks in Fig. 7(b) indicate the thermally activated relaxation process, and the peak positions at different temperatures can be described by using Eq. (10).
where, the symbol f0 represents the preexponential factor, KB denotes the Boltzmann constant, and Ea represents the activation energy.
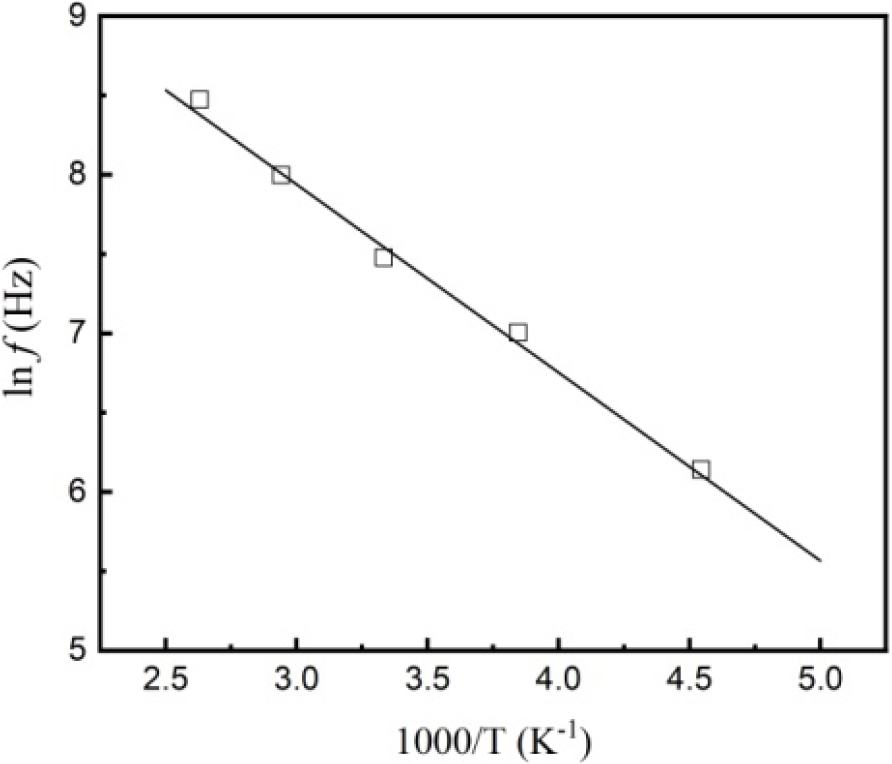
Fig. 8 presents the Arrhenius plot between the position of the relaxation peak and the reciprocal of temperature (1/T). By linear fitting, the value of Ea was extracted to be about 0.83 eV. The obtained value agrees well with the reported activation energy of the exchange of electrons between Ti3+ and Ti4+ ions.29)
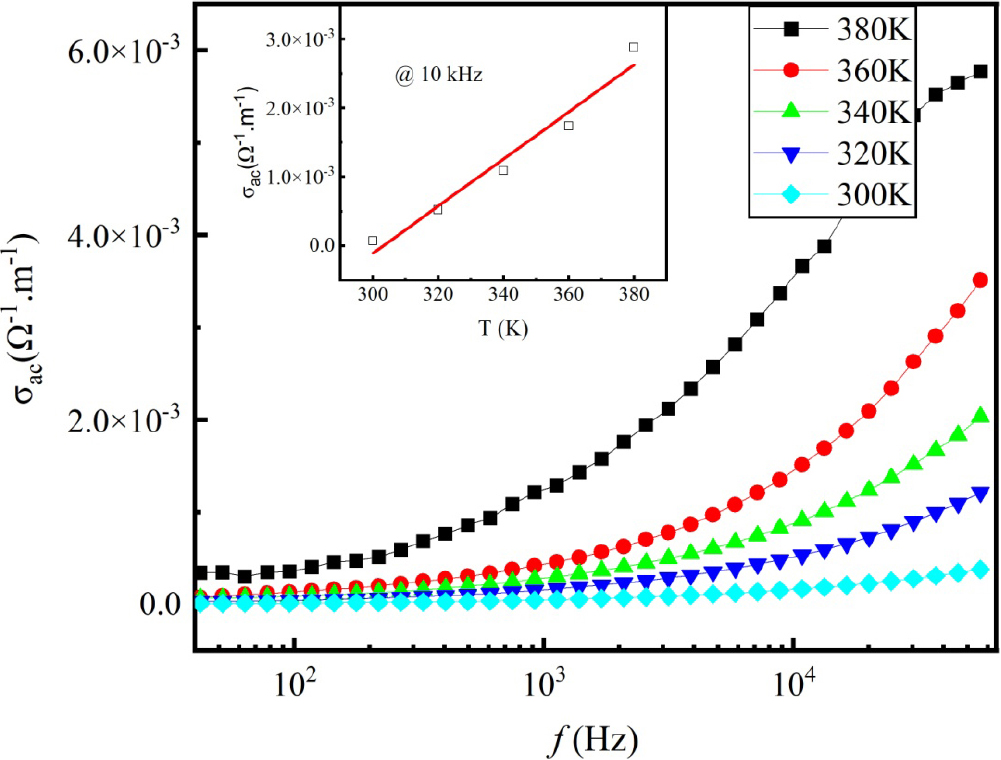
The AC conductivity (σac) can be obtained by using the formula σас = 2πƒε0ε′tanδ. Fig. 9 shows the typical results of variation of σac with frequency for BANT04 above the room temperature (300~380 K), and the inset displays typical values of σac at a fixed frequency f = 10 kHz. The solid line is the linear fit. It is clear that the conductivity behavior of the sample exhibits a semiconductor characteristic, which means the value of σac increases as the temperature or frequency increases. Based on the jump conduction process, the increase of σac with the increase of temperature may be due to the thermally activated electron jump between the Nb5+ and Ti4+ ions at the octahedral location and the hole jump between Ti4+ and Al3+ ions in the prepared composite sample. As mentioned above, since conduction occurs through electron jumps between Nb5+ and Ti4+ ions and hole jumps between Ti4+ and Al3+ ions, electrons that traverse the grain boundary through a jumping mechanism will accumulate at this interface owing to their elevated resistivity. Consequently, the resultant space charge polarity leads to an enhancement in the dielectric constant.30) Nevertheless, the research revealed that resistive grain boundaries exhibit greater efficiency when operating at lower frequencies. The enhancement of σac may be attributed to the presence of low porosity. Similar results can be obtained for the BANT06 and BANT08 samples.
4. Conclusion
Perovskite-type oxide materials Ba(Al0.5Nb0.5)xTi1-xO3 (x = 0, 0.04, 0.06, 0.08) were prepared using standard solid-state reaction method to investigate the effect of quadrivalent and trivalent elements co-doping on the dielectric and electric modulus properties. XRD profiles indicate that the Al+Nb co-doping into BaTiO3 does not change the crystal structure significantly with the doping concentration up to 8 %. The doping ions exist as Al3+ and Nb5+ chemical state, revealed by the XPS data. The maximum dielectric constant and low dielectric loss were obtained at the dopant concentration x = 0.04. The AC conductivity exhibits a semiconductor characteristic as a result of the thermally activated electron jump conduction process. The temperature and frequency dependence of the dielectric and electric modulus properties implies a quasi-electric dipoles behavior. The results offer valuable insights into the influence of B-site co-doping on the dielectric and electric modulus properties of BaTiO3-based ceramics and hold relevance for the advancement of new electronic devices.