1. 서 론
지속 가능한 에너지 하베스팅 기술에 대한 다양한 연구는 가속화되는 기후 위기를 막기 위한 노력의 일환으로 계속되고 있다. 이 노력은 기후 위기의 주요 원인인 온실 가스 배출을 줄이는데 상당한 기여를 했다.1,2) 친환경 에너지 하베스팅 기술 중 하나인 열전 기술은 화석 연료의 연소 없이 폐열로부터 직접 전기를 생산할 수 있어 많은 관심을 받고 있다.3,4,5) 열전 장치의 효율은 장치에 사용된 재료의 열전 성능지수(zT)와 밀접하게 연결되어 있다. 따라서 열전재료의 zT를 증가시키는 것은 중요하다. zT (=S2σT/κ)는 제벡계수(S), 전기전도도(σ), 온도(T) 및 열전도도(κ)에 의존한다. κ는 전하에 의한 열전도도(κe)와 격자 열전도도(κl)의 합으로 나타낼 수 있다.6,7) zT에서 S2σ를 파워팩터(power factor, PF)라고 하며 이는 재료의 전자 수송 특성을 결정하는 주요 지표이며, PF가 높고 κ가 낮을수록 zT는 높아진다.
저온 폐열 발전용 열전 재료는 상온 주변의 높은 변환 효율로 잘 알려져 있으며 웨어러블 전자제품의 전원으로 활용하기 위해 연구 중이다. 최적의 저온 열전 재료 중 하나인 비스무트 텔루라이드(Bi2Te3)는 좁은 밴드 갭(~0.15 eV)을 가지고 좋은 전기적 특성을 가지고 있다.8,9,10) Bi2Te3에 원소를 합금 혹은 도핑함으로써 그 전기적 성능을 더욱 향상시킬 수 있다.11,12) Cu는 특히 n-형 Bi2Te3 기반 합금의 κl를 낮춰 zT를 향상시키는 데 중요한 원소이며, 많은 연구에서 Cu가 포함된 Bi2Te3의 결정구조가 안정해져 재현성이 확보되었다고 보고했다.13,14,15,16,17)
Sie 등18)은 n-형 Bi2Te3에 Cu 1.0 wt%를 첨가하여 PF가 증가하고 κ가 감소한 결과를 보고했다. 그들의 연구에서 Bi2Te3와 비교했을 때, 상온 zT 값은 0.31에서 0.60으로 증가했다. Kim 등19)의 연구에서 Cu 첨가로 강화된 점 결함 포논 산란의 효과로 상온에서 Cu0.02Bi2Te3의 zT가 ~0.68로 증가했으며, Lognone와 Gascoin20)의 연구에서 Cu 첨가로 낮아진 κ로 인해 상온에서 ~0.7의 zT를 얻었다. Chen 등21)은 n-형 Bi2Te2.7Se0.3에 Cu를 0.02몰 첨가하여 홀 농도(nH)와 홀 이동도(µH)의 증가를 확인했고, 결론적으로 상온에서 zT ~0.7, 420 K에서 최고 zT ~1.05를 가졌음을 보고했다.
이 연구에서 우리는 n-형 Cu0.008Bi2Te3 샘플의 밴드 파라미터를 two-band (TB) 모델을 통해 계산하고 300 K, 520 K에서 밴드 갭(Eg)이 변화할 때 전기적 특성, κ, 이론 최대 zT의 변화를 분석했다.22) Cu0.008Bi2Te3 조성 선정의 근거는 선행 연구 결과에 기반한다. n-형 CuxBi2Te2.7Se0.3조성에서 Cu 첨가량(x)을 0.006에서 0.012까지 변화시킨 연구에서, x = 0.008일 때 가장 우수한 열전성능을 나타내어 300 K에서 zT = 0.73을 달성하였다.17) 이러한 실험적 결과를 토대로, 본 연구에서는 재현성이 확보되고 높은 열전성능을 보이는 Cu0.008Bi2Te3을 기본 조성으로 선택하여 Eg 변화에 따른 최대 zT를 예측하고자 하였다. Cu0.008Bi2Te3 샘플의 측정 결과 300 K에서 zT ~0.41, 520 K에서 zT ~0.46이었으며, Tauc plot으로 얻은 optical 밴드 갭은 ~0.13eV이었다. 상태밀도 유효 질량(md*), deformation potential (Edef), 격자 열전도도(κl), 페르미 준위는 실험값으로부터 계산한 값으로 고정하고 Eg만을 0.1에서 0.3 eV로 변화시키며 그 효과를 분석했다. 이때 저온과 고온에서의 결과 비교를 위해 300 K, 520 K에서의 데이터로 계산했다. TB 모델 계산 결과, 모든 온도에서 Eg가 0.1에서 0.3 eV로 증가할 때 PF는 증가하고, κ는 감소하여 zT가 증가하는 결과를 보였다. 그 변화폭은 300 K에서보다 520 K에서 더 컸는데, 이는 고온에서 증가하는 바이폴라 효과에서 기인한 것이다. 결론적으로, 520 K에서 Eg가 0.3 eV로 변하면 zT ~0.61을 가질 것이며, nH가 최적화되었을 때 예상되는 이론 최대 zT는 ~0.75로 계산되었다. 우리의 연구는 Cu0.008Bi2Te3의 Eg가 증가하면 이론 최대 zT가 향상될 수 있음을 시사한다. 나아가 좁은 Eg를 가지는 열전 재료의 Eg가 증가했을 때 PF가 증가하고, κ는 감소하여 zT가 증가할 수 있음을 이론적으로 확인했다.
2. 실험 방법
Cu0.008Bi2Te3의 합성은 진공 석영관에서 전통적인 반응법으로 제조하였다. 고순도의 원료인 Bi (99.999 %, 5N Plus), Te (99.999 %, 5N Plus), Cu (99.999 %, KRT Lab)를 화학량론적으로 계량 후 석영관에 넣고 진공 10-5 Torr에서 밀봉하였다. 석영관에 밀봉된 원료를 1,323 K에서 6시간 동안 가열하고, 그 온도에서 12시간 동안 유지한 후, 점차적으로 실온까지 냉각하였다. 반응 완료 후, 얻어진 금속 잉곳을 Ar 분위기에서 고에너지 볼 밀링(SPEX 8000D, SPEX SamplePrep)으로 분말화하였다. 이후, 703 K에서 5분 동안 70 MPa의 압력 하에 진공(10-6 Torr)에서 스파크 플라즈마 소결(spark plsama sintering, SPS, SPS-1030, Sumitomo Coal Mining Co., Ltd.)을 통해 측정용 벌크 샘플을 얻었다.
Cu0.008Bi2Te3의 σ 및 S는 열전 특성 측정 시스템(ZEM-3M8, Advance Riko)을 사용하여 측정했다. 이때 온도차는 5, 10 및 15 K이었다. 홀 효과 측정 장비(HMS-5300, Ecopia)를 이용하여 300 K에서 nH 및 µH를 측정하였다. 시료의 광학 Eg는 UV-vis 측정(Lamda 365+, Perkinelmer) 결과를 통해 추정하였다. 총 열전도도는 다음 식을 통해 계산하였다: κ = α ‧ ρs ‧ Cp, 여기서 α, ρs 및 Cp는 각각 열확산도, 시료 밀도 및 비열용량이다. α는 레이저 플래시 분석기(laser flash analysis, LFA, Netzsch)의 측정을 통해 얻었다. Cu0.008Bi2Te3의 Cp는 108.06 + 5.53 × 10-2 J mol-1 K-1의 공식에 의해 결정되었다.23) Cu0.008Bi2Te3의 ρs는 7.834 g cm-3의 측정값을 사용했다.
Single parabolic band (SPB) 모델을 이용하면 S는 아래의 식 (1)로 표현된다. 여기서 kB, e, η는 각각 볼츠만 상수, 전자의 전하량, 페르미 준위이며 차수 j에 대한 페르미 적분[Fj(η)]은 식 (2)로 표현된다.24)
페르미 준위로 결정되는 S [식 (1)]와 식 (3)을 이용하면 S 측정값을 통해 L을 쉽게 구할 수 있다[식 (4)].24)
Snyder 등25)은 S와 σ를 이용해 가중 이동도(µW)를 구하는 식을 제시했다. 그들에 따르면 (µH)는 아래 식 (5)로 계산할 수 있다.
또한 µW를 이용하면 식 (6)을 통해 B-factor를 계산할 수 있다.25)
TB 모델을 이용하면 S, σ, 및 홀 상수(RH)를 아래의 식 (7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18)으로 구할 수 있다.25) 이때 아래첨자 maj, min은 각각 major밴드, minor밴드를 의미한다. 이 논문에서는 n-형 Cu0.008Bi2Te3의 데이터를 토대로 계산하였으므로 major 밴드는 conduction 밴드, minor 밴드는 valence 밴드를 나타낸다.
TB 모델에서 S, σ는 각각 아래 식 (7, 8)로 구할 수 있다.26)
이때 Smaj, Smin는 각각 major 밴드의 S, minor 밴드의 S를 나타내며 식 (9, 10)으로 구할 수 있다.26)
여기서 사용된 Δ는 kBT 단위의 Eg를 의미하며, 식 (11)로 계산되는 값이다.26)
식 (7, 8)의 σmaj, σmin은 각각 major 밴드의 σ, minor 밴드의 σ이며, 식 (12, 13)으로 계산된다.26)
여기서 h는 플랑크 상수이고, µ0는 비축퇴 이동도로 major 밴드와 minor 밴드 모두 식 (14)로 계산할 수 있다.26)
여기서 Cl은 elastic 상수로 74 GPa를 사용하여 계산했다.27)
식 (15)를 통해 RH를 구할 수 있고, 이때 RH,maj는 major 밴드의 RH [식 (16)], RH,min은 minor 밴드의 RH [식 (17)]를 나타낸다.26)
식 (15, 16, 17)로부터 구한 RH를 이용하면 nH를 구할 수 있다[식 (18)].26)
Cu0.008Bi2Te3와 같이 Eg가 작은 재료의 경우 κe와 κe 뿐만 아니라 바이폴라 열전도도(κbp) 또한 고려해야 한다. TB 모델에서 κe와 κl는 아래 식 (19, 20, 21, 22)를 통해 구할 수 있다. 이렇게 계산한 κe, κbp를 κ에서 빼면 κl를 구할 수 있다.26)
3. 결과 및 고찰
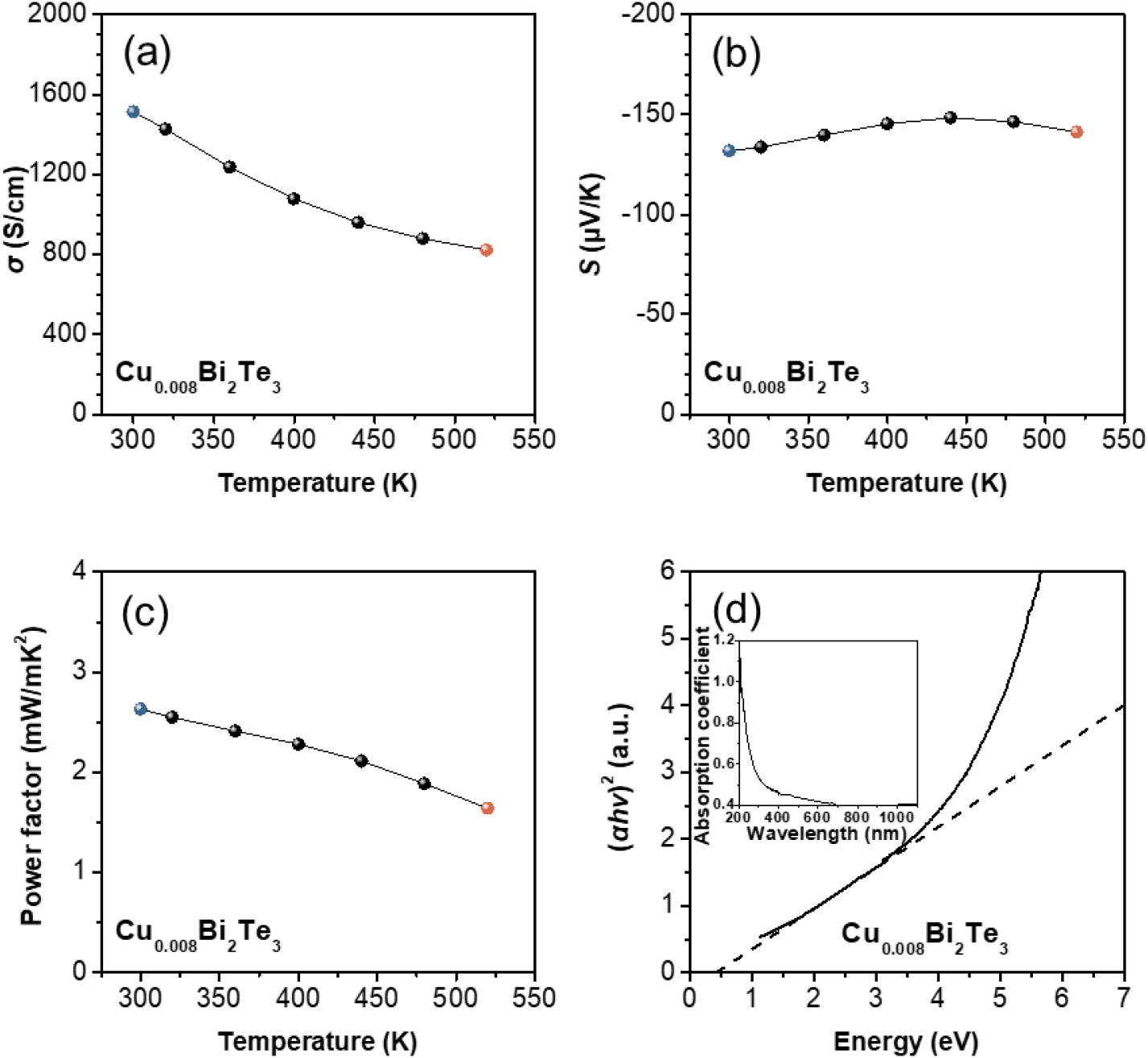
Fig. 1은 Cu0.008Bi2Te3의 열전 특성 측정값을 보여준다. Fig. 1(a)는 온도에 따른 σ 측정값을 나타냈다. 이후 TB 모델을 적용시켜 계산한 300 K 측정값은 파란색, 520 K 측정값은 빨간색으로 표시했다. 저온과 고온 각각에서 나타나는 Eg 변화의 효과를 보기 위해 두 온도에서 계산을 진행했다. σ는 온도가 증가함에 따라 감소하는데, 이는 반도체 물질의 전형적인 특성이다. σ는 온도가 300 K에서 520 K로 증가할 때 1,513 S cm-1에서 822 S cm-1로 감소한다. Fig. 1(b)는 온도에 따른 S 측정값을 나타냈다. 모든 온도 구간에서 n-형 전도 특성을 보인다. S는 온도에 따라 증가하다가 440 K 이상 온도에서 감소하는 경향을 보이는데, 이는 고온 구간에서 바이폴라 효과가 나타남을 시사한다.22) 구체적으로 300 K에서 -131.8 µV K-1이던 S는 440 K까지 온도가 증가할 때 -148.4 µV K-1으로 증가하다가 온도가 520 K로 증가함에 따라 다시 -141.2 µV K-1로 감소한다. 고온 바이폴라 효과는 온도 상승에 따라 conduction 밴드의 전자들이 충분한 열에너지를 얻어 valence 밴드로 여기되면서 발생한다. 이 과정에서 conduction 밴드의 전자(n-형)와 valence 밴드의 정공(p-형)이 동시에 전도에 참여하게 되며, 이들은 서로 반대 방향으로 이동하면서 S에 반대로 기여한다. 또한 전자-정공 쌍의 재결합 과정에서 발생하는 에너지는 열전도도를 증가시켜, 결과적으로 고온에서의 열전성능이 저하된다. Fig. 1(c)는 온도에 따른 PF를 보여준다. 온도에 따라 증가하다가 감소하는 S의 변화폭이 작기 때문에 PF는 σ와 같이 온도 증가에 따라 감소하는 경향을 보인다. 300 K에서 2.63 mW m-1 K-2이던 PF는 온도 증가에 따라 점차 감소하다 520 K에서 1.64 mW m-1 K-2의 값을 가진다. Fig. 1(d)는 Tauc plot을 나타내며, inset으로 파장에 따른 흡광도를 나타냈다. 이때 α, h, ν는 각각 흡수 계수, 플랑크 상수, 광자의 진동 수를 의미한다. Tauc plot의 실선은 측정값을 나타냈으며, 측정값이 상승하는 지점에서 추세선을 점선으로 그려 optical Eg를 유추했다. Tauc plot으로 얻은 optical Eg는 ~0.13 eV로 문헌 값(~0.15 eV)보다 조금 작은 값으로 측정되었다.10)
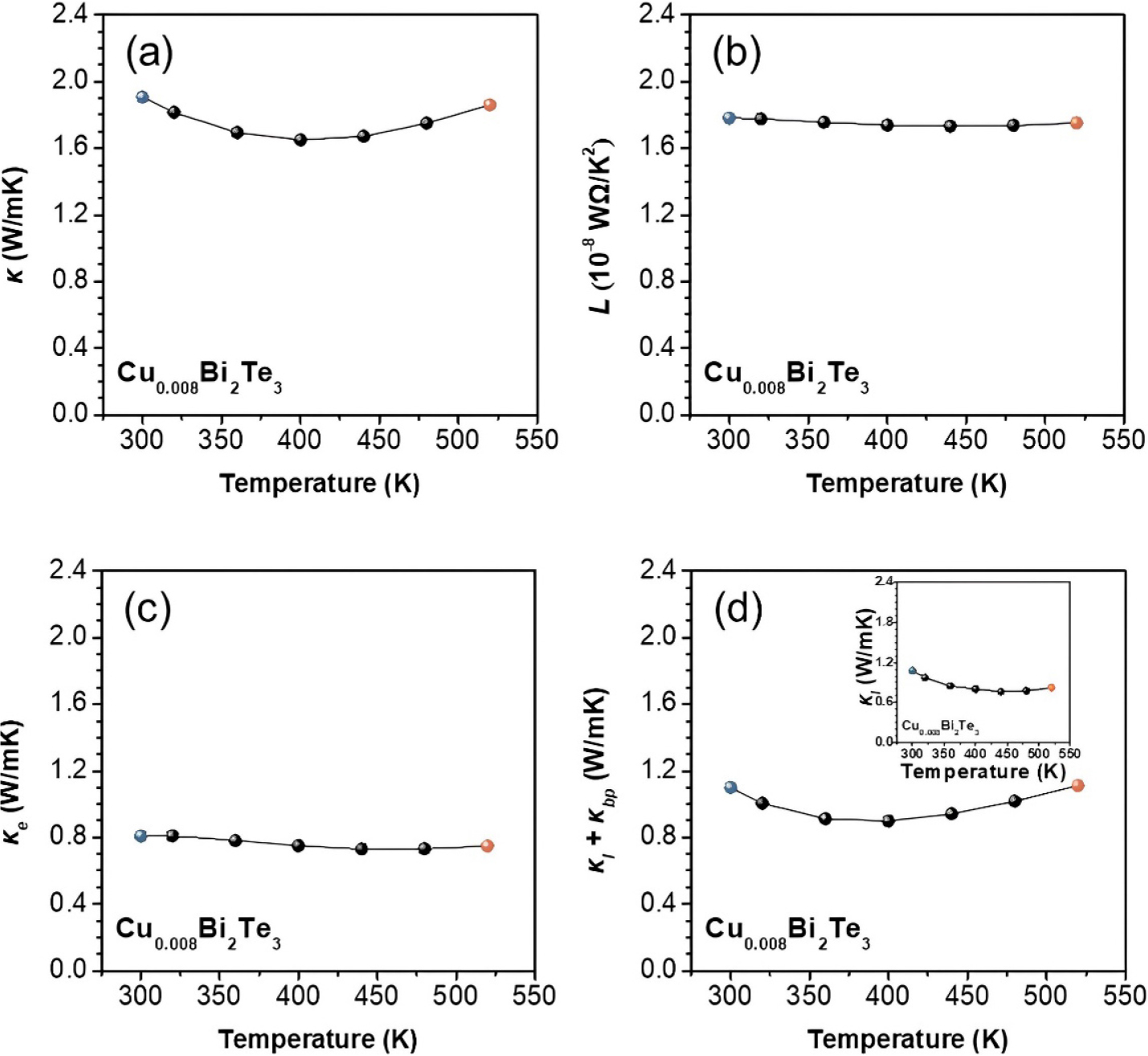
Fig. 2(a)는 온도에 따른 κ 측정값을 보여준다. κ는 온도 증가에 따라 감소하다가 증가하는 것을 볼 수 있는데, 이 또한 고온 구간에서 일어나는 바이폴라 효과에서 기인한 결과이다. 바이폴라 효과에 의해 전자와 정공이 동시에 열전도에 관여해 열전도도가 증가한 것이다. 이를 바이폴라 효과로 인한 열전도도를 κbp라고 한다. κ는 300 K에서 400 K까지 온도가 증가할 때 1.91 W m-1 K-1에서 1.65 W m-1 K-1로 감소한다. 이후 온도가 더 증가함에 따라 증가하는 κ는 520 K에서 1.86 W m-1 K-1의 값을 가진다. Fig. 2(b)는 식 (4)를 이용해 계산한 L이다. 측정한 S로부터 구한 η로 L을 구했다. 온도에 따라 S가 증가 후 감소함에 따라 L은 감소 후 증가하는 결과를 보인다. 구체적으로 온도가 300 K에서 440 K로 증가할 때 L은 1.78 × 10-8 W Ω K-2에서 1.73 × 10-8 W Ω K-2으로 감소하다가, 온도가 520 K로 증가할 때 1.75 × 10-8 W Ω K-2로 다시 증가한다. Fig. 2(c)는 κe를 보여준다. 이때 κe는 Wiedemann-Franz law (κe =L σ T)를 기반으로 계산한 결과이다. 온도에 따른 κe는 대체적으로 감소하는 경향을 보인다. 300 K에서 Cu0.008Bi2Te3의 κe는 0.81 W m-1 K-1이고, 520 K에서 κe는 0.75 W m-1 K-1이다. Fig. 2(d)는 κe에서 κe를 뺀 κl + κbp를 보여주며, Fig. 2(d)의 inset에 κl를 나타냈다. κl + κbp와 κl는 온도에 따라 감소하다가 증가하는 경향을 보인다. 이는 κbp가 대체적으로 T-1에 비례하기 때문이다. 예를 들어, κl + κbp는 온도가 300 K에서 400 K로 증가할 때 1.09 W m-1 K-1에서 0.89 W m-1 K-1로 감소하다가 520 K로 온도가 더 증가하면 1.11 W m-1 K-1로 증가한다. 반면, κl는 온도가 300 K에서 440 K로 증가할 때 1.07 W m-1 K-1에서 0.76 W m-1 K-1로 감소하다가 520 K로 온도가 더 증가하면 0.82 W m-1 K-1로 증가한다. 이는 κbp가 온도가 증가함에 따라 0.02 W m-1 K-1에서 0.29 W m-1 K-1로 점진적으로 증가했기 때문이다.
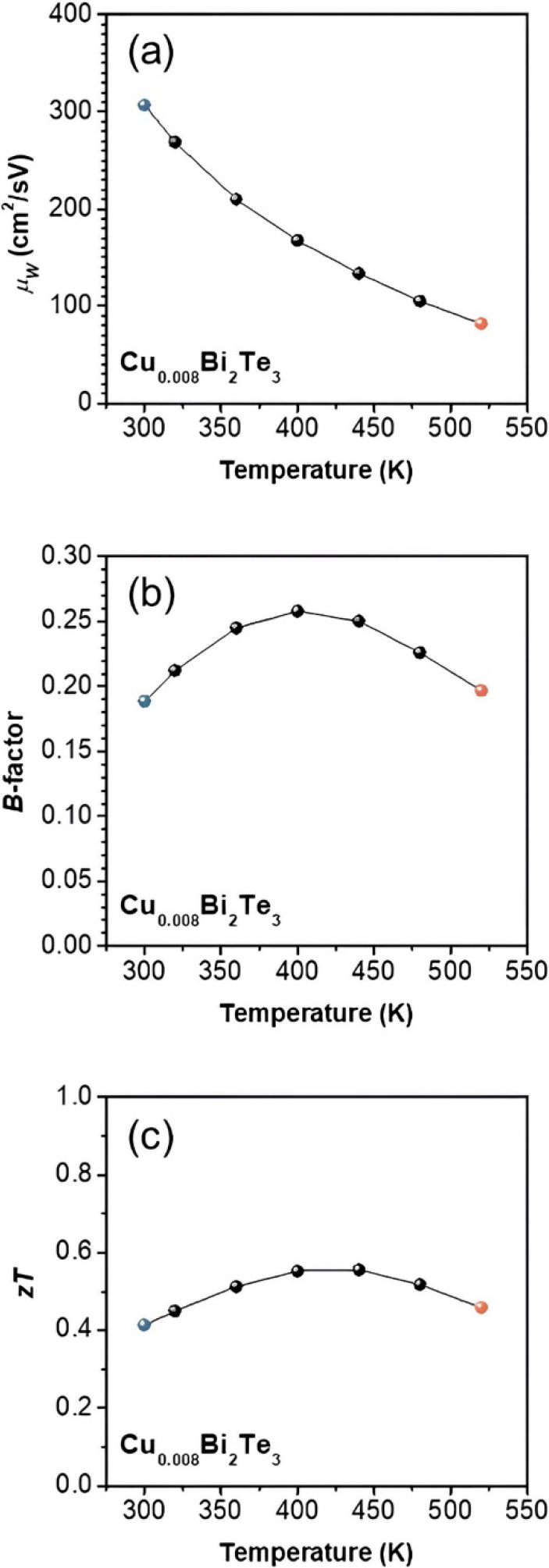
Fig. 3(a)는 식 (5)로 계산한 온도에 따른 µW를 보여준다. Cu0.008Bi2Te3의 µW는 온도 증가에 따라 감소하는 경향을 보인다. 구체적으로 300 K에서 307.03 cm2 V-1 s-1이던 µW는 520 K에서 81.97 cm2 V-1 s-1로 감소한다. µW를 통해 이론 최대 PF를 예측할 수 있는데, 온도 증가에 따라 감소하는 µW를 통해 온도 증가에 따라 이론 최대 PF 또한 감소할 것을 예상할 수 있다. Fig. 3(b)는 식 (6)으로 계산한 온도에 따른 B-factor를 보여준다. 계산된 B-factor는 온도 증가에 따라 증가하다가 감소하는 것을 볼 수 있다. 구체적으로 300 K에서 0.19이던 B-factor는 온도가 400 K일 때, 0.26의 최고 B-factor를 보이고, 이후 520 K로 온도가 증가하면 0.20으로 다시 감소한다. 본 연구의 Cu0.008Bi2Te3는 기존에 보고된 n-형 Bi2Te3의 B-factor (300 K에서 0.11, 520 K에서 0.05) 대비 높은 값을 나타냈다.28) B-factor는 µW에 비례하고 κl에 반비례하는 값으로, 이론적 최대 zT를 결정하는 주요 인자이다. Cu0.008Bi2Te3의 κl는 상온에서는 기존 Bi2Te3와 유사하나, 고온에서는 더 낮은 값을 보였다.28) 또한, Cu 도핑으로 인한 밴드의 유효질량 증가로 인해 Cu0.008Bi2Te3의 µW가 기존 Bi2Te3 대비 향상되었다. 앞서 µW를 통해 이론 최대 PF를 예측할 수 있었던 것과 같이 B-factor를 통해 이론 최대 zT를 예측할 수 있다. Cu를 첨가하지 않은 n-형 Bi2Te3에 비해 Cu0.008Bi2Te3의 B-factor가 높게 계산된 결과를 통해 Cu0.008Bi2Te3의 이론 최대 zT가 더 높을 것임을 예측할 수 있다. Fig. 3(c)는 온도에 따른 zT 측정값을 보여준다. zT는 온도가 300 K에서 440 K로 증가함에 따라 증가하다가 온도가 520 K로 증가하면 감소하는 경향을 보인다. 결과적으로 zT는 온도 증가에 따라 0.41에서 0.56으로 증가한 후 0.46으로 다시 감소한다. 이처럼 좁은 밴드 갭을 가지고, 고온 구간에서 바이폴라 효과가 있는 물질들에 대해서 TB 모델을 이용하면 major 밴드와 minor 밴드의 효과를 함께 고려하여 밴드 파라미터를 계산할 수 있다. 이 연구에서 n-형 Cu0.008Bi2Te3의 특성을 계산하였기에, conduction 밴드가 major 밴드, valence 밴드가 minor 밴드이다. Cu0.008Bi2Te3의 Eg 변화에 따른 열전 특성 변화를 예측하고, 특히 온도에 따라 바이폴라 효과가 어떻게 작용하는지 알아보기 위해 TB 모델을 이용했다.
Table 1에 300 K에서의 nH, µH 측정값과 식 (23)을 이용해 계산한 md*를 나타냈다.29)
Table 1.
300 K carrier concentration, hall mobility and density-of-states effective mass of Cu0.008Bi2Te3.
|
nH (cm-3) |
µH (cm2 V-1 s-1) |
md* (m0) | |
| Cu0.008Bi2Te3 | 4.27E+19 | 224.20 | 0.93 |
상온에서 홀 측정 장비로 측정한 nH는 4.27 × 1019 cm-3, µH는 224.2 cm2 V-1 s-1이었다. 측정한 값으로 계산한 md*는 0.93 m0로 문헌 값과 유사한 값이다.29)
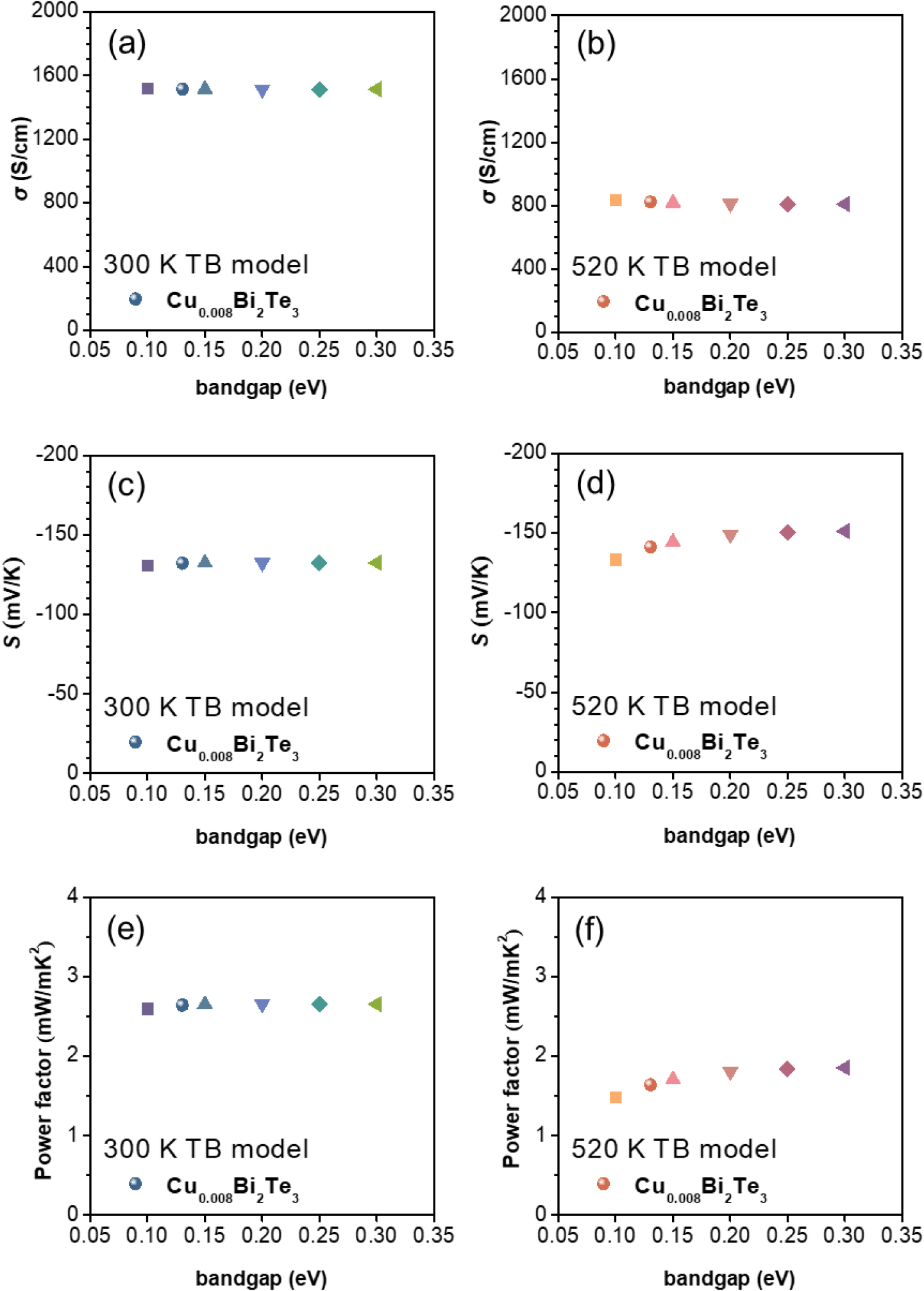
Fig. 4는 TB 모델로 계산한 밴드 갭(Eg) 변화에 따른 전기적 특성 변화를 나타냈다. 계산에 사용한 피팅 파라미터 md*, Edef는 Table 2에 나타냈다. 300 K에서의 md,CB*, md,VB*, Edef,CB, Edef,VB는 각각 0.931 m0, 1.057 m0, 19.68 eV, 22 eV를 사용했다. 반면, 520 K에서의 md,CB*, md,VB*, Edef,CB, Edef,VB는 각각 0.636 m0, 1.057 m0, 28.92 eV, 22 eV를 사용했다. Figs. 4, 5, 6에 나올 Eg 변화에 따른 TB 모델 계산 값은 각 온도의 md,CB*, md,VB*, Edef,CB, Edef,VB는 Table 2의 값을 사용하고, Eg만을 변화시켜 계산한 결과이다. 이때 열전 재료로 유망한 반도체 재료들의 Eg가 대부분 0.05~0.3 eV인 것을 참고하여 Eg는 0.05 eV 간격으로 0.1 eV에서 0.3 eV로 변화시키며 계산했다.27)Fig. 4(a)는 300 K에서 Eg 변화에 따른 σ 변화 양상을 보여준다. 300 K에서의 실험값 σ는 파란색으로 표시했다. Eg가 0.1 eV에서 0.3 eV로 변화함에 따라 σ는 소폭 감소한다. 이는 Eg가 증가함에 따라 높아진 에너지 장벽으로 캐리어의 이동이 어려워지기 때문이다. 예를 들어, Eg가 0.1 eV일 때 σ가 1,516.4 S cm-1, 그리고 Eg가 0.3 eV일 때 σ가 1,513.2 S cm-1로 변한다. Fig. 4(b)는 520 K에서의 Eg 변화에 따른 σ를 나타낸다. 520 K에서의 σ 측정값을 빨간색으로 나타냈다. 온도에 따른 바이폴라 효과의 변화를 보기 위해 300 K와 520 K 두 온도에서 계산을 진행했다. 300 K에서의 σ 변화와 같이 520 K에서도 Eg가 증가할 때 σ는 감소한다. 하지만 300 K에서의 감소폭보다 520 K에서의 감소폭이 더 큰 것을 볼 수 있다. 이는 고온에서 바이폴라 효과로 전자 이동이 더욱 어려워지기 때문이다. 520 K에서 Eg가 0.1 eV에서 0.3 eV로 변할 때 σ는 835.8 S cm-1에서 810.6 S cm-1로 감소한다. 300 K에서 σ 감소폭은 0.2 %인 반면 520 K에서 σ 감소폭은 3 %로 520 K에서의 감소폭이 300 K에서보다 약 15배 크다. 두 온도에서 모두 σ는 Eg가 커짐에 따라 감소하는 것으로 보아 전기전도도의 측면에서 Eg는 작아질 때 더 유리하다는 것을 알 수 있다. 이는 식 (8, 12, 13)을 통해 알 수 있는데, σ는 σmaj와 σmin의 합으로 이루어진다. 이때 Eg가 작아야 σmin가 커지므로 Eg가 작은 것이 σ의 측면에서 유리한 것을 알 수 있다.
Table 2.
Fitting parameters (md,CB*, md,VB*, Edef,CB, Edef,VB) of Cu0.008Bi2Te3 at 300 K and 520 K.
| Cu0.008Bi2Te3 | 300 K | 520 K |
| CB density-of-states effective mass (md,maj*) | 0.931 | 0.636 |
| VB density-of-states effective mass (md,min*) | 1.057 | 1.057 |
| CB deformation potential (Edef,maj) | 19.68 | 28.92 |
| VB deformation potential (Edef,min) | 22 | 22 |
Fig. 4(c)는 300 K에서의 Eg 변화에 따른 S 계산 값을, Fig. 4(d)는 520 K에서의 Eg 변화에 따른 S 계산 값을 보여준다. 300 K와 520 K에서 S는 Eg 증가에 따라 증가하는 경향을 보인다. σ의 경우와 같이, S 또한 520 K에서의 변화폭이 더 크다. 300 K에서 Eg 변화에 따라 S는 -130.8 µV K-1에서 -132.4 µV K-1로 1.9 %만큼 증가하는 반면, 520 K에서는 -133.2 µV K-1에서 -151.2 µV K-1로 12.7 %만큼 증가한다. 520 K에서의 S 변화량은 300 K에서보다 약 6배 큰 값이다.
Fig. 4(e)는 300 K에서 Cu0.008Bi2Te3의 Eg 변화에 따른 PF 계산 결과를 보여준다. 300 K에서 PF는 Eg 증가에 따라 소폭 증가한다. Cu0.008Bi2Te3의 Eg 변화에 따라 σ는 감소했지만, S가 증가했기 때문에 PF도 증가하는 경향을 보인다. Cu0.008Bi2Te3의 Eg가 0.1 eV에서 0.3 eV로 증가함에 따라 PF는 2.59 mW m-1 K-2에서 2.65 mW m-1 K-2로 증가한다. 300 K에서 Cu0.008Bi2Te3의(Eg ~0.13 eV) 실험 PF가 2.64 mW m-1 K-2인 것에 비해 Eg가 0.3 eV로 증가하면 PF는 0.3 % 증가한 값을 가질 수 있다. Fig. 4(f)는 520 K에서 Eg 변화에 따른 PF 계산 결과를 보여준다. Cu0.008Bi2Te3의 Eg가 0.1 eV에서 0.3 eV로 증가할 때, PF는 1.48 mW m-1 K-2에서 1.85 mW m-1 K-2로 약 1.25배 증가한다. 520 K에서 Cu0.008Bi2Te3의 실험 PF 1.63 mW m-1 K-2에 비해 약 13 % 증가한 값이다. 고온에서의 PF 증가폭이 상온에서보다 더 큰 것은 440 K 이상의 온도 구간에서 생기는 바이폴라 효과가 감소했기 때문이다.
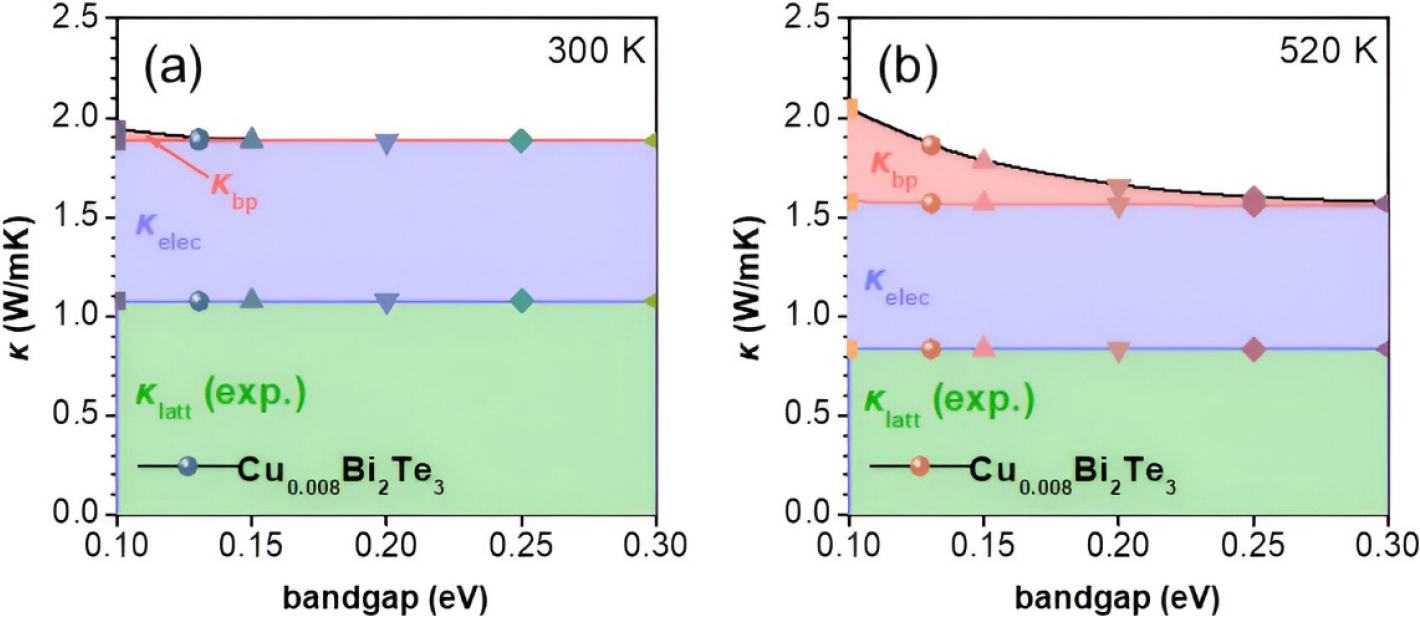
Fig. 5(a, b)는 각각 300 K, 520 K에서의 Cu0.008Bi2Te3의 Eg 변화에 따른 κ 계산 결과를 보여준다. 두 온도에서 모두 Eg가 증가할 때 κ는 감소하는 경향을 보인다. 300 K에서 κl는 Fig. 2(d) inset의 1.07 W m-1 K-1으로 고정하여 계산한 결과이다. 300 K에서 Eg가 증가할 때 κe는 0.2 % 정도로 적게 감소하지만 κbp는 64.7 % 가량 크게 감소한다. 따라서 급격히 감소하는 κbp로 인해 κ가 감소하는 결과가 나온다. 구체적으로 Eg가 0.1 eV에서 0.3 eV로 증가할 때 κe와 κbp는 각각 0.809 W m-1 K-1에서 0.808 W m-1 K-1, 0.056 W m-1 K-1에서 8.641 × 10-5 W m-1 K-1로 감소한다. 520 K에서는 κl를 Fig. 2(d) inset의 0.83 W m-1 K-1으로 고정하여 계산했다. 520 K에서 Eg가 0.1 eV에서 0.3 eV로 증가할 때 κe와 κbp는 각각 0.745 W m-1 K-1에서 0.725 W m-1 K-1, 0.467 W m-1 K-1에서 0.015 W m-1 K-1로 감소한다. 520 K에서의 κe와 κbp는 각각 약 2.7 %, 96.8 % 감소한다.
300 K에서 κ는 Eg 변화에 따라 1.94 W m-1 K-1에서 1.88 W m-1 K-1로 변하는 것에 비해 520 K에서 κ는 2.05 W m-1 K-1에서 1.57 W m-1 K-1로 변화한다. Fig. 2의 전기적 특성과 같이 고온에서의 변화폭이 더 큰 것을 알 수 있다. 고온에서의 TB 모델 계산 결과를 보면 κbp의 감소가 눈에 띄게 나타난다. 이전 보고된 연구에서 가중 이동도 비율, Eg, 그리고 nH의 증가가 κbp의 감소를 야기한다고 설명했다.24) 우리의 계산에서 밴드 파라미터가 고정되었기 때문에 κbp의 증가 혹은 감소는 Eg와 nH의 변화에 의한 것임을 알 수 있다. 같은 Eg를 가질 때 300 K에서보다 520 K에서 κbp의 값이 더 크게 계산되었는데 고온에서 열에 의한 캐리어 이동도 증가 혹은 에너지 장벽 감소 등의 이유로 바이폴라 현상이 두드러지기 때문이다. 식 (11)에 의하면 kBT 단위의 밴드 갭 Δ는 온도가 높을 때 더 작은 값으로 계산된다. 따라서 고온에서의 바이폴라 효과가 더 두드러지게 되는 것이다.
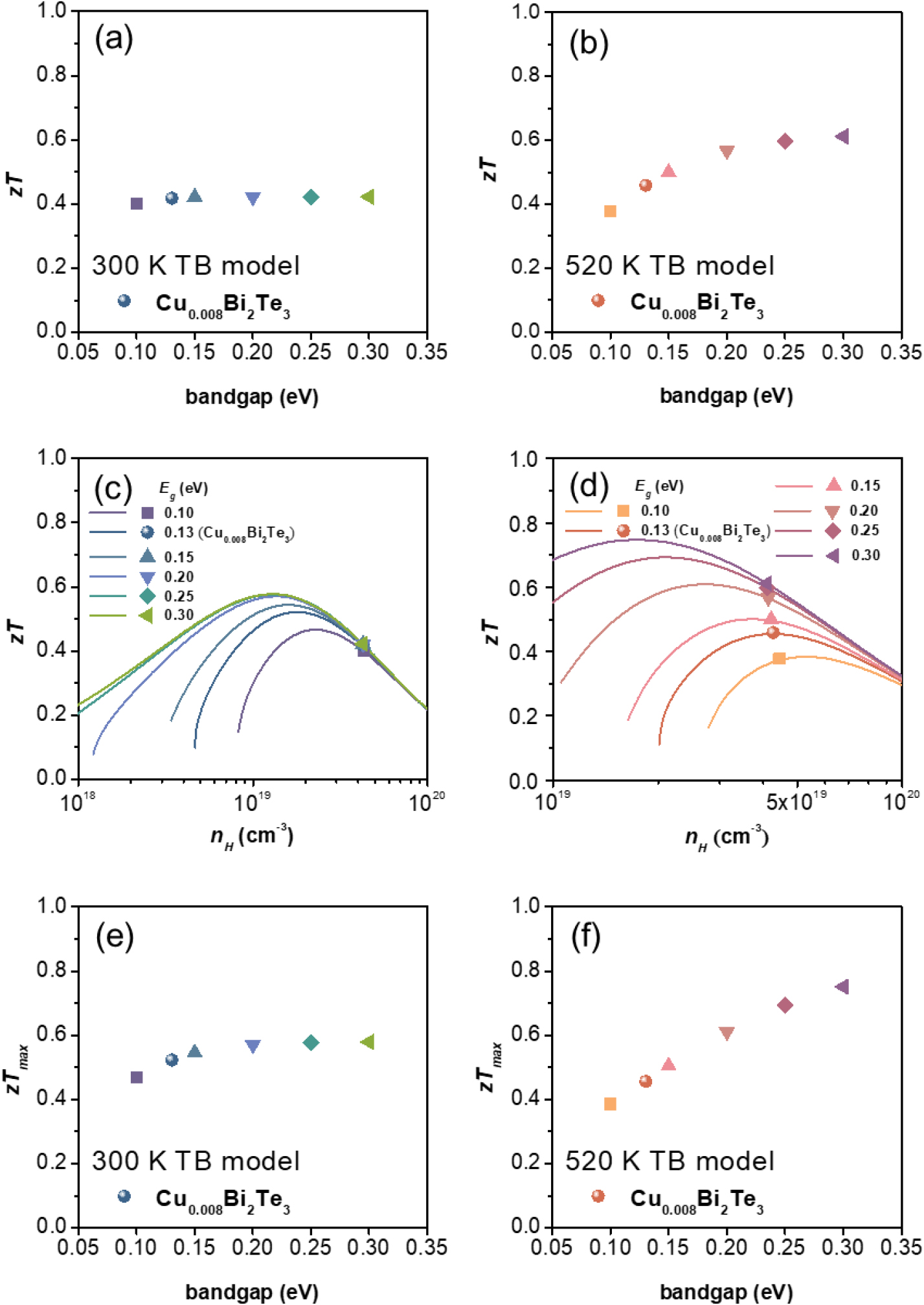
Fig. 6(a)는 300 K에서 계산한 Eg 변화에 따른 zT를 보여준다. Eg가 0.1 eV에서 0.3 eV로 변화할 때 PF가 증가하고 κ가 감소한 결과에서 예상할 수 있었듯 zT는 Eg 증가에 따라 증가하는 경향을 보인다. 상온에서 PF의 증가폭과 κ의 감소폭이 크지 않았기 때문에 zT의 증가폭도 크지 않다. Eg가 0.1 eV와 0.3 eV일 때, zT는 각각 0.40과 0.42로 계산됐다. 이는 Eg가 0.1 eV에서 0.3 eV로 증가할 때 zT가 약 5 % 증가한 결과이다. Fig. 6(b)는 520 K에서 계산한 zT 결과를 보여준다. 300 K에서의 결과에 비해 520 K에서 PF 증가폭과 κ 감소폭이 컸기에 zT 증가폭도 300 K에서보다 크게 계산됐다. 구체적으로 Eg가 0.1 eV에서 0.3 eV로 증가할 때, zT는 0.37에서 약 65 % 증가하여 0.61의 값을 가진다.
Fig. 6(c, d)는 각 온도에서 TB 모델로 계산된 nH에 따른 zT 곡선과 특정 페르미 준위에서의 계산값을 나타낸다. Cu0.008Bi2Te3 샘플의 광학적 측정으로 얻은 Eg (~0.13 eV)를 기준으로, TB 모델 피팅을 통해 도출된 conduction 및 valence 밴드의 md,CB*, md,VB*, Edef,CB, 그리고 Edef,VB (Table 2)를 µ0,CB(orVB) [식 (14)]에 적용하였다. 이를 통해 conduction 및 valence 밴드의 전기전도도[σCB, σVB, 식 (12, 13)]를 계산하고, 최종적으로 총 전기전도도(σ)를 도출하였다[식 (8)]. η를 -2에서 3까지 변화시키며, 동일한 Eg 조건에서 conduction 및 valence 밴드의 제벡계수[SCB, SVB, 식 (9, 10)]를 계산하고 총 제벡계수(S)를 구하였다[식 (7)]. 같은 방식으로 conduction 및 valence 밴드의 Lorenz number [LCB, LVB, 식 (20, 21)]를 계산하여 κe [식 (19)]와 κbp [식 (22)]를 도출하였다. 이러한 계산된 변수들을 바탕으로 zT를 산출하였다. nH는 동일한 η 범위에서 식 (15, 16, 17, 18)을 통해 계산되었으며, Fig. 6(c, d)는 각 η값에 대한 nH와 zT의 관계를 보여준다. 이를 통해 다른 변수들을 고정한 상태에서 Eg 변화가 nH에 따른 zT 거동에 미치는 영향을 분석할 수 있다.
고정된 페르미 준위에서 Eg가 증가할 때 nH는 감소한다. 예를 들어, 300 K에서는 4.28 × 1019 cm-3에서 4.26 × 1019 cm-3으로, 520 K에서는 4.45 × 1019 cm-3에서 4.10 × 1019 cm-3으로 감소한다. TB 모델로 계산한 nH에 따른 zT 곡선을 보면 곡선의 최고점이 나타나는 nH가 Eg 증가에 따라 감소하는 것을 볼 수 있다. 300 K에서 nH가 1.0 × 1019 cm-3에서 2.0 × 1019 cm-3사이 값으로 조정되었을 때 이론 최대 zT를 가질 수 있다. 반면 520 K에서 이론 최대 zT를 가질 수 있는 nH는 2.0 × 1019 cm-3에서 5.0 × 1019 cm-3사이 값이다.
nH가 조정되었을 때 얻을 수 있는 이론 최대 zT를 Fig. 6(e, f)에 나타냈다. Eg가 증가할 때 이론 최대 zT도 증가하며, 300 K보다 520 K에서 더 증가 폭이 더 큰 것을 볼 수 있다. Eg가 0~0.15 eV인 구간에서는 520 K의 이론 최대 zT보다 300 K의 이론 최대 zT가 더 크지만, 0.2 eV이상인 구간에서는 520 K에서의 이론 최대 zT가 더 큰 것을 볼 수 있다. 300 K와 520 K에서 Eg가 0.3 eV일 때의 이론 최대 zT는 각각 0.58과 0.75로 계산됐다. 이는 실험 값에 비해 각각 11 %, 67 % 증가한 결과이다.
4. 결 론
본 연구에서는 TB 모델을 이용하여 n-형 Cu0.008Bi2Te3의 밴드 갭 조절이 열전 성능에 미치는 영향을 분석하였다. 실험 결과, 300 K, 520 K에서 zT 값이 각각 ~0.41, ~0.46으로 나타났으며, 광학적 밴드 갭은 ~0.13 eV였다. 실험 결과를 토대로 상태밀도 유효 질량(md*), deformation potential (Edef), 격자 열전도도(κl), 페르미 준위를 고정하고 밴드 갭을 0.1에서 0.3 eV까지 변화시키면서 TB 모델 계산을 수행하였다. 그 결과, 300 K와 520 K에서 밴드 갭이 증가함에 따라 파워팩터(PF)는 증가하고 열전도도는 감소하여 zT 값이 향상되는 것을 확인하였다. 특히, 520 K에서 증감의 폭이 더 크게 계산되었으며, 이는 고온에서 바이폴라 효과가 두드러지기 때문이다. 본 연구 결과는 Cu0.008Bi2Te3의 밴드 갭을 증가시킴으로써 열전 성능을 크게 향상시킬 수 있음을 시사한다. Cu0.008Bi2Te3의 밴드 갭이 0.3 eV일 때 520 K에서 zT 값은 ~0.61까지 증가할 것으로 예측되었으며, 최적의 홀 농도에서 이론적 최대 zT 값은 ~0.75로 계산되었다. 이 연구는 좁은 밴드 갭을 가진 반도체형 열전 재료의 밴드 갭이 증가되면 열전 성능이 증가할 수 있음을 시사한다.