1. 서 론
플랜트 구조물 엔지니어링에서 사용되는 합금들은 높은 열전도도 및 낮은 비열 특성으로 인해 급격한 온도 상승에 대한 내화성이 낮다. 이러한 내화성 문제는 주로 합금의 기계적 및 열적 특성에 따라 달라지게 된다. 강도, 탄성 계수, 크리프를 포함하는 기계적 특성과 열전도율, 열팽창과 같은 열적 특성이 플랜트 구조물의 화재 반응에 영향을 주는 대표적인 요인이다.1)
따라서, 우수한 강도, 용접성 및 부식/내후성 특성을 가지고 있는 고강도 저합금강을 주로 사용하고 있다. 저합금강은 합금 원소 Mn (manganese), Si (silicon), Cu (copper), Ni (nickel), Cr (chromium), P (phosphorus)를 기반으로 하는 합금원소 총량이 5 wt% 미만인 강을 말한다.2,3) 특히, 고강도 저합금강은 가격이 저렴하고 기계적 강도가 우수하여 해상 및 육상 구조물 엔지니어링 플레이트 분야에서 필수적인 철강소재이다.4,5) 저합금강은 플랜트 엔지니어링 분야에 활용될 때 강판을 용접하는 방법으로 조립되고 있다.6) 하지만, 열전도율과 열팽창률이 높아 용접부에 균일한 열 압력 유지가 어려워 번스루 현상 및 뒤틀림이 발생하는 문제가 있다.7) 그러므로, 플랜트 엔지니어링에 사용되는 저합금강은 고강도 및 고인성 뿐만 아니라 저열전도도, 저열팽창 특성을 가져야 한다.
철은 본질적으로 α-Fe가 풍부한 합금이며 V및 Ti와 같은 철의 특성을 개선하기 위해 소량의 다른 합금 농도를 포함하여 철의 기계적 특성을 개선하고 입자 크기를 낮출 수 있다.8,9,10) 기존 연구에서는 기계적 특성에 대한 용질 원자의 합금화 효과의 중요성에도 불구하고 대부분의 연구는 주로 고강도 저합금강의 제조, 마모, 변형, 경도, 파괴에 초점을 맞춰져 있으며,11,12,13) 용질원자 종류와 함량에 따른 기계적 및 열팽창 특성에 대한 이론적 연구에 대한 보고는 거의 없었다.
본 연구에서는 제1원리 계산을 사용하여 무질서한 α-Fe 기반 고용체 합금의 기계적 및 열적 특성을 연구하였다. 저합금강의 특성을 이해하기 위해서 Fe1-xMx (M = Sc, Ti, V, Cr, Mn, Co, Ni, Cu, Zn) 이원계 합금상에 대한 용질원자와 X = 0.02, 0.05, 0.1 at%을 첨가한 모델을 사용하여 함량 변화에 대한 합금 효과를 조사하였다. 모든 합금조성에 대해서 열역학적 안정성을 평가하고 경험식을 사용하여 연성(ductility), 이론적 비커스 경도(theriacal Vicker’s hardness), 나사전위(screw dislocations) 에너지 계수, 모서리전위(edge dislocations) 에너지 계수, 열팽창계수(coefficient of thermal expansion)를 계산하였다. 이 논문이 내마모성, 저열전도율과 저열팽창을 모두 갖춘 플랜트 엔지니어링 소재 개발에 가이드 라인을 제시할 수 있을 것이라 기대한다.
2. 계산 방법
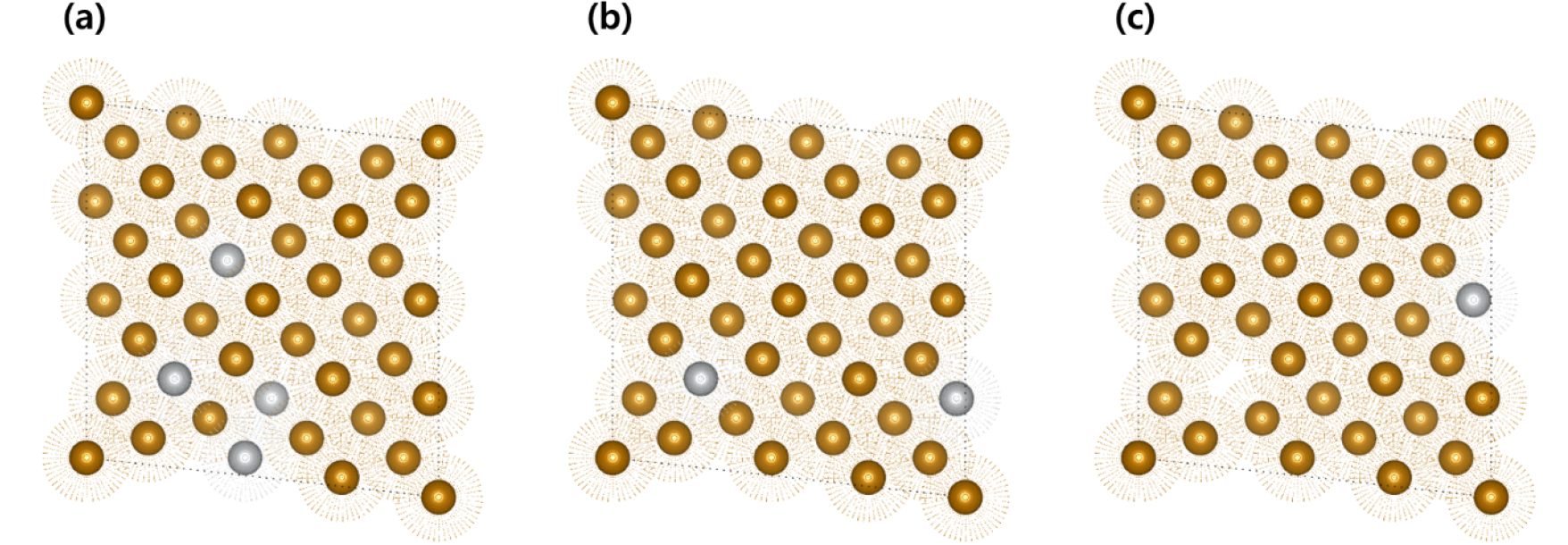
본 연구에서는 Fe1-xMx 합금의 물성을 연구하고자 전자밀도이론(density functional theory)을 기반으로 한 제1원리 계산을 수행하였다. 모든 계산은 VASP (vienna ab initio simulation package) 코드로 계산되었다.14) 기계적 및 열팽창 특성을 계산하기 위하여 GGA (generalized gradient approximation)와 Perdew-Burke-Ernzerhof (GGA-PBE) 교환상관함수를 사용하였다.15,16) α상 기반의 Fe1-xMx (x = 0.02, 0.05, 0.1) (M = Sc, Ti, V, Cr, Mn, Co, Ni, Cu, Zn)함량에 따른 원자간 화학적 무질서의 영향을 고려하기 위해 SQSs (special quasirandom structures) 모델들을 ATAT 코드를 사용하여 모사하였다.17,18) 계산에 사용된 SQSs 합금 구조모델은 Fig. 1에 모식도에 나타내었다. Brillouin zone 적분은 Monkhorst k-points pack grid를 사용하였다.19,20) 5 × 5 × 5의 k-point 조건으로 SQSs 모델을 구조최적화 하였다.21) 탄성상수는 구조최적화보다는 조금 더 높은 9 × 9 × 9를 각각 사용하여 탄성상수 계산을 수행하였다. 계산의 정확도를 향상시키기 plane wave cutoff energy (500 eV)를 사용하였으며, 전자 에너지는 10-6 eV, 그리고 각 구조 모델의 반복 계산 횟수는 최종 계산 결과와 전회에 얻은 결과 간 에너지 차이가 0.02 eV/Å 이하로 수렴해 가는지 여부에 따라 결정하였다.22) 모든 계산은 spin-polarized를 사용하였다.23) 합금의 탄성 특성을 계산하기 위해 stress-strain relation을 사용하였다. 또한, 정확한 탄성 특성을 측정하기 위해 최적화된 구조 모델에는 각각 두 방향으로 6개의 변형률(±0.005, ±0.008, ±0.01)을 부여하였다. 계산된 탄성 상수는 Voight-Reuss-Hill 가정에 따른 식 (3), (4), (5), (6), (7)을 기반으로 부피탄성계수(bulk modulus, B) 및 전단탄성계수(shear modulus, G), 영률(Young’s modulus, E)을 도출하는데 활용되었다.24) 또한, Poisson’s ratio (ν), Pugh’s constant (G/B) 이론적 비커스 경도(Hv), 나사전위(Kscrew) 및 모서리 전위(Kedge) 에너지 계수는 이론적 탄성계수 데이터를 활용한 식 (9), (10), (11), (12)를 사용하여 계산하였다.25,26,27,28,29,30)
위의 식에서 Bv, BR, Gv, GR는 각각 Voigt, Reuss으로 계산된 부피 탄성계수와 전단계수이며, 최종적인 B, G 값은 Hill 식으로 나타내었다. 온도에 따른 열팽창 계수는 Debye-Grüneisen 모델을 사용하여 계산하였다.31) 따라서 다음 방정식을 사용하여 디바이 온도와 부피 사이의 관계를 설명하였다.32)
위의 식에서 θD는 디바이온도, N은 원자의 개수 및 kB는 볼츠만 상수이다.
3. 결과 및 고찰
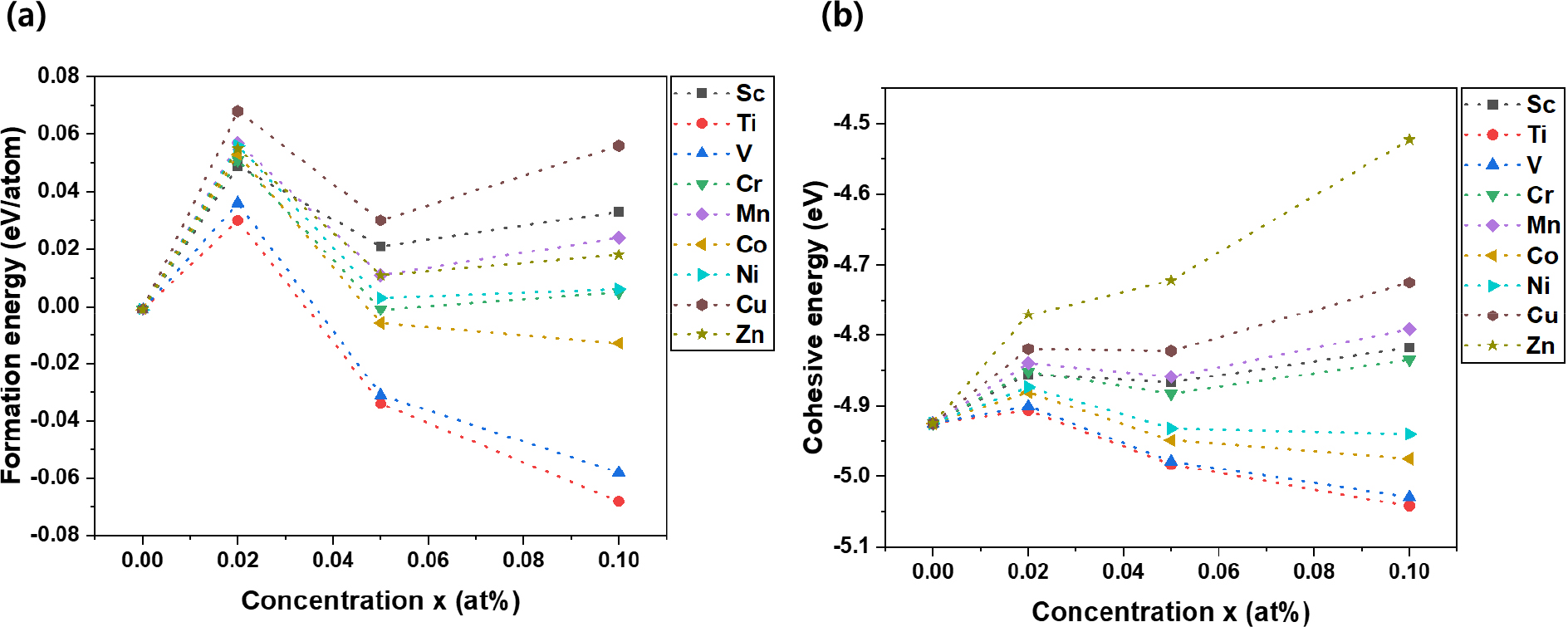
계산된 Fe1-xMx 합금의 형성에너지(formation energy), 응집에너지(cohesive energy)를 Fig. 2에 나타내었다. 형성에너지는 물질의 상 변화에 따른 안정성을 확인하는 지표이다. 또한 응집에너지는 화합물의 모든 원자들이 서로 분리되어 결합이 끊어질 때 필요한 전체 에너지를 말한다.33) 형성에너지가 0에 가깝거나 양의 값을 가져 불안정한 합금을 만든다.34) 형성에너지는 0.02 at%의 Ti와 V를 제외하고 용질원자 함량이 증가함에 따라서 α-Fe보다 증가하였다. 그러나 Ti와 V의 경우 0.05 at% 이상에서 α-Fe보다 낮아지는 것을 볼 수 있었다. 즉, 소량의 용질원자 첨가는 불안정한 합금을 이루므로 활성화 에너지 이상의 에너지 상태에서 원소 분리가 일어날 수도 있다. 본 논문에서는 엔트로피의 영향을 고려하지 않고 계산하였으며, 합금을 형성하기 위한 높은 온도에서는 엔트로피 안정화 효과가 증가하여 합금 형성에 유리해진다. 모든 용질원자는 순수한 Fe보다 0.02 at% 함량에서 응집에너지가 높으나, 0.05 at%와 0.1 at% 함량에서는 Ti, V, Co 및 Ni는 응집에너지가 α-Fe보다 낮으므로 결합을 끊을 때 많은 에너지가 필요한 것으로 예상된다. 따라서 가장 안정한 합금은 Fe-Ti, Fe-V, Fe-Co, Fe-Ni라는 것을 알 수 있었다.
저합금강의 구조적 특성에 대한 용질 원자의 다양한 합금 효과를 확인하기 위해서 용매격자에 대한 용질원자의 영향을 알아야 한다. 따라서 α-Fe의 특성에 대한 합금 효과에 대해 분석하였다. Table 1에 계산된 이원계 합금의 용질 원자 종류와 함량에 따른 이론적인 격자상수와 3개의 독립적인 탄성상수를 나열하였다. 모든 용질 원자는 α-Fe의 격자상수를 증가시킨다. 또한, 용질 원자 첨가 함량에 따라 3개의 탄성상수에 대한 비선형 합금 효과를 갖는다는 것을 발견하였다. 그리고 용질 원자의 첨가에 따라 C12과 C44가 감소하는 것을 관찰하였다. 사용된 방법의 정확도와 α-Fe 및 이원계 합금의 단결정 탄성산수에 대한 합금 효과는 기존 연구와 거의 비슷한 경향을 보인다.35,36) 이는 최적의 k-point mesh가 선택되었으며, 계산결과의 신뢰성을 보여준다.
Table 1.
The calculated lattice constant (a in Å) and elastic constant (GPa) of Fe1-xMx alloys.
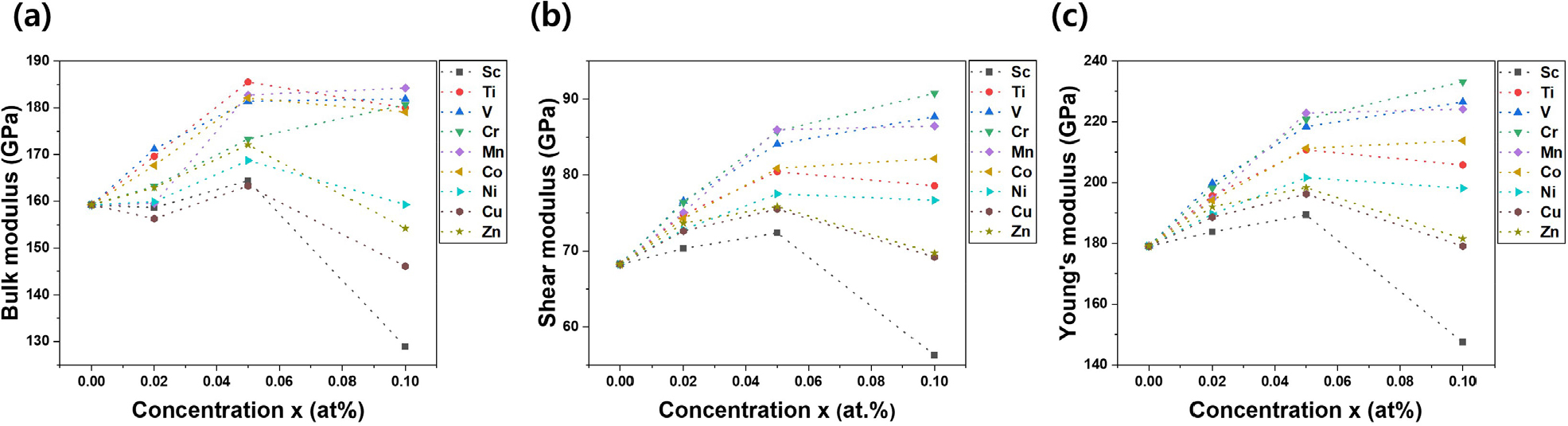
Fig. 3(a-c)는 계산된 이원합금의 부피 탄성계수, 전단 탄성계수 및 영률에 대한 값들을 비교한 그래프이다. 계산된 이원계 합금의 부피 탄성계수, 전단 탄성계수 및 영률은 이전의 논문과 비교하여 큰 오차가 없는 것으로 확인하였다.36,37,38,39) 부피 탄성계수의 경우 Ti, V, Co, Cr 용질원자가 첨가되었을 경우 함량이 증가할수록 향상되었다. 하지만, Zn의 경우 0.05 at%까지는 증가하다가 0.1 at%부터 감소하는 것을 관찰하였다. 이와 반대로 Sc, Ni, Cu는 함량이 증가할수록 감소하는 것을 알 수 있었다. 부피 탄성계수의 경우 외부 압력에 대한 저항력을 의미하며 일반적으로 전자의 밀도와 비례하는 값을 보이므로, 금속원소의 최외각 전자의 수 차이에 따라 변화가 발생하는 것으로 판단된다. 전단 탄성계수와 영률은 첨가된 모든 용질 원소에서 0.02~0.05 at%까지 증가하는 것을 볼 수 있었다. 하지만, 0.1 at% 함량에서 V, Cr, Co를 제외하고 모두 감소하는 것을 관찰하였다. 전단 탄성계수와 영률은 모두 결합 강도에 영향을 받으며, 기계적 특성에 직접적인 영향을 주는 것으로 알려져 있다.40) 공통적으로 부피 탄성계수, 전단 탄성계수와 영률에서 V, Cr, Mn 용질원자가 첨가된 합금이 모두 높은 값을 보여주는 것을 확인할 수 있었다. 따라서 전반적으로 V, Cr, Mn 용질원자가 0.1 at%가 첨가된 경우 기계적 강도가 더 우수할 것으로 예상된다.
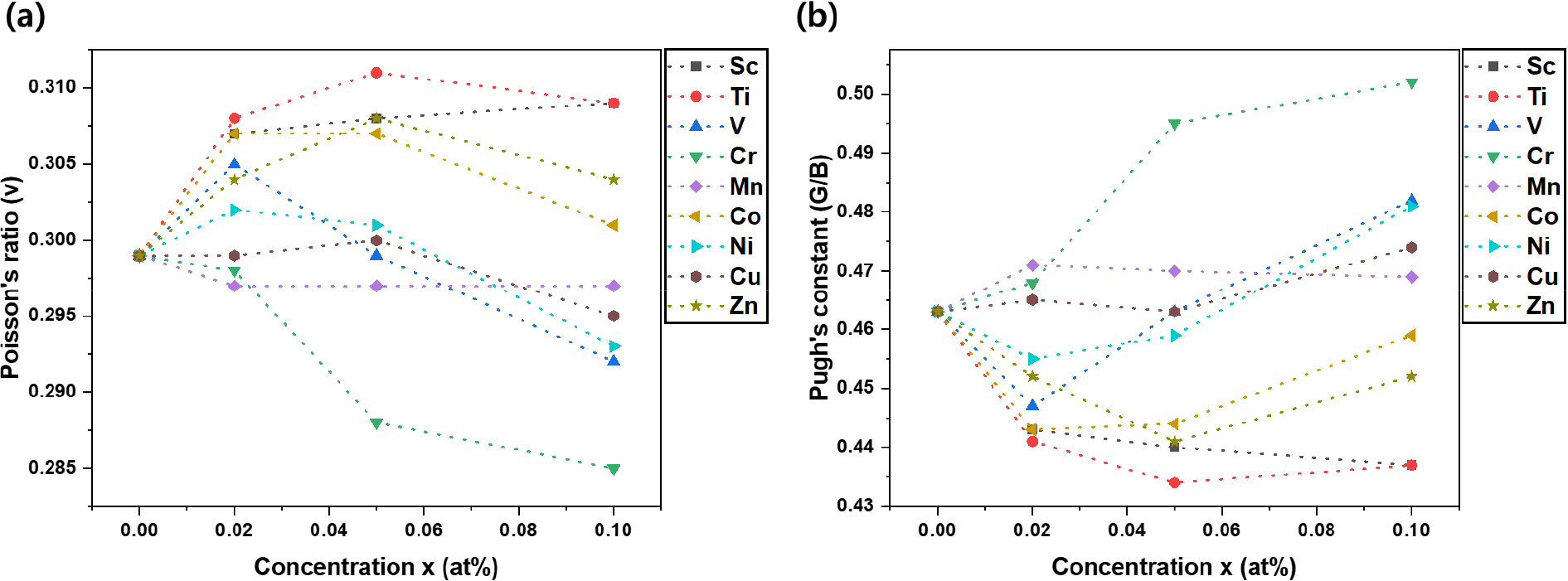
Fig. 4는 첨가된 용질 원자종류에 따른 이원 합금의 Pugh’s constant (G/B)와 Poisson’s ratio (ν)의 비교결과를 나타내었다. 일반적으로 재료의 연성과 취성은 경험적 지표를 사용하여 평가한다. 탄성계수와 전단계수사이의 Poisson’s ratio와 G/B가 지표로 많이 사용된다. G/B는 탄성계수와 전단계수와 관련된 전위 이동과 결합 균열 사이의 경쟁을 관찰하는 것이다. 등방성 재료의 경우 Poisson’s ratio를 사용하며, 0.26보다 클 때 연성을 나타낸다. 일반적으로 다결정 재료는 G/B가 0.57보다 클 때 연성을 나타낸다. Poisson’s ratio에서 고려된 용질 원자의 첨가량이 0.1 at%일 때 연성특성이 약해지는 것을 볼 수 있었다. 하지만, Ti, Sc, Co, Ni, Zn 용질원자는 함량에 상관없이 순수한 α-Fe보다 연성이 강한 것을 알 수 있다. G/B는 V, Cr, Ni, Mn, Cu 용질원자가 첨가되었을 때 첨가량과 상관없이 순수한 α-Fe보다 연성이 강해지고, Cr를 0.1 at% 첨가하였을 때 가장 큰 연성을 보였다. 이러한 공통점에서 α-Fe의 고유 연성이 Cr, Ni 용질원자에 따라 가장 많이 향상됨을 알 수 있다.
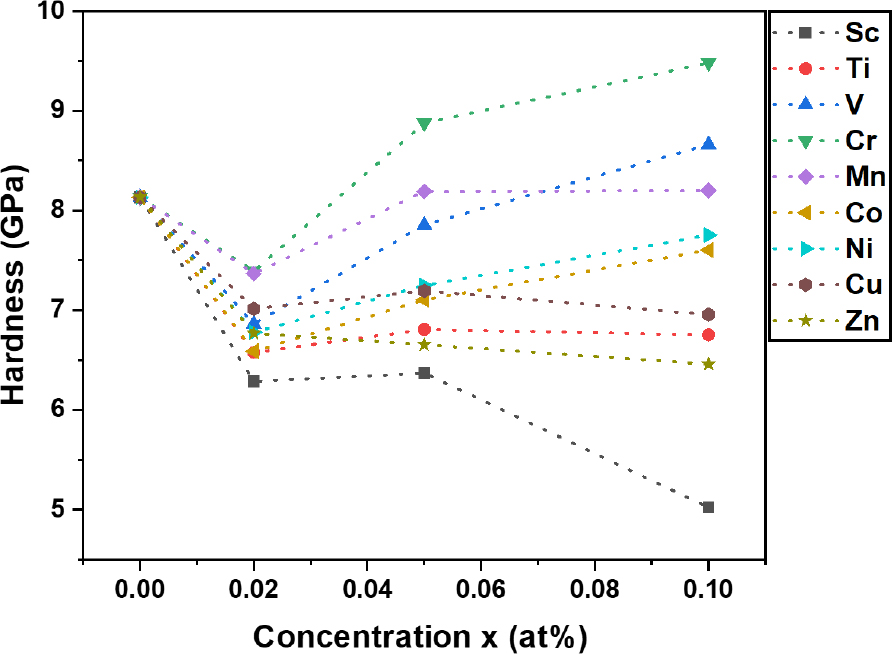
경도는 구조 재료의 성능에 중요한 특성이다. 경도는 탄성 또는 소성변형에 저항하는 재료의 특성을 나타내며, 재료의 연성, 항복응력 및 강도와 관련이 있다.41)Fig. 5는 bcc구조의 Fe1-xMx 이원 합금의 원소와 함량 변화에 따른 이론적 경도를 나타내었다. 모든 원소에서 0.02 at%를 첨가하였을 경우 경도가 감소하였다. 하지만, Fe1-xMx 합금에 V, Cr, Mn을 0.05 at% 및 0.1 at% 이상 첨가하면 경도가 증가하였다. 이 결과는 적은 양의 원소를 첨가하면 경도가 감소하지만 V, Cr, Mn의 경우 일정수준 이상 첨가할 경우 오히려 경도를 증가시켜 내마모성을 강화시킬 수 있음을 의미한다.
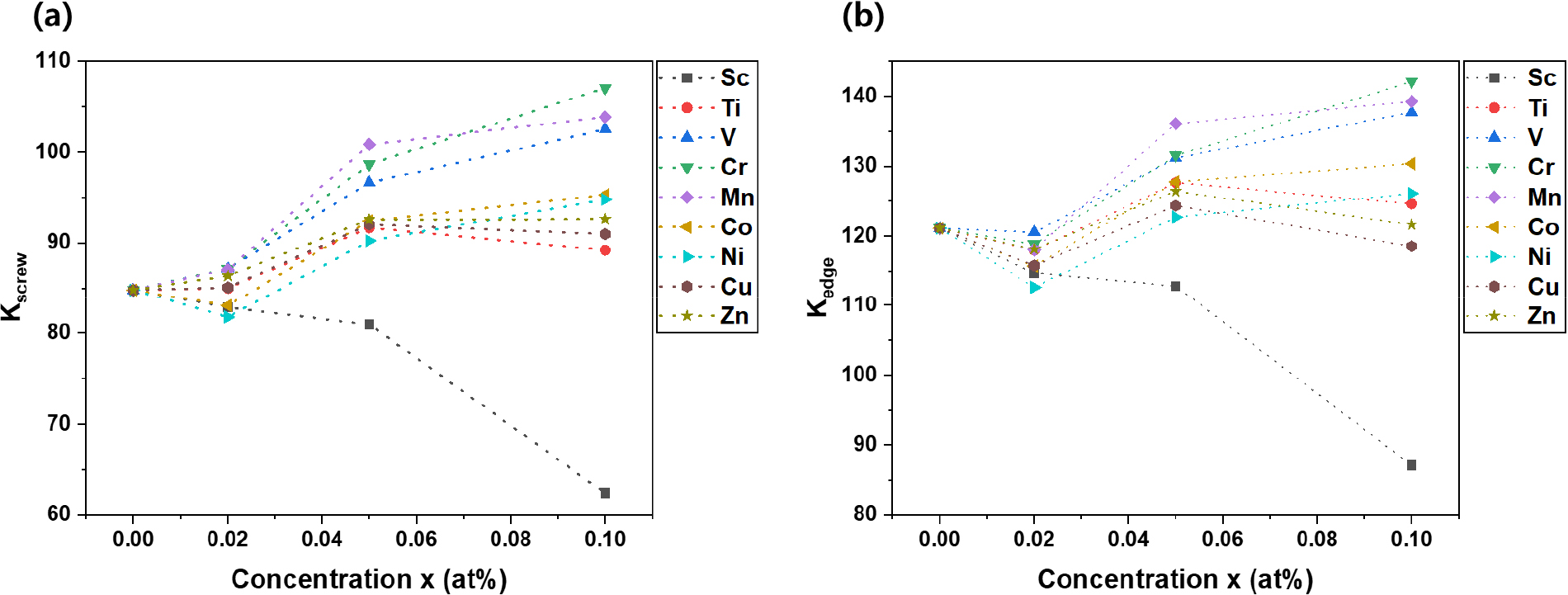
재료의 소성 특성을 평가하기 위해 전위 핵 생성 능력을 조사하기 위해 에너지 계수(K)를 분석하였다. Fig. 6(a, b)는 Fe1-xMx합금의 나사전위 및 모서리 전위의 K를 나타내었다. 전위가 탄성체를 한 평면에서 절단하여 발생한다고 가정하면 전위선의 단위 길이 당 에너지는 K에 따라 달라진다.28)
나사전위에서 Cr, Mn, Zn용질원자를 제외하고 나머지 원소들은 0.02 at%이 첨가되면 감소하였으며, Sc는 첨가량에 상관없이 전위 에너지가 감소하는 것을 볼 수 있었다. 하지만, 8개의 용질 원자는 0.05~0.1 at% 함량에 따라 K가 증가함을 보여준다. 0.05 at% 이상에서 α-Fe보다 나사전위 및 모서리전위가 증가하는 것은 전위 핵 생성이 용질원자 함량증가에 따라 전위가 발생되지 않는 것이 선호됨을 나타낸다.42) 또한, 모든 이원계 합금은 나사전위의 K가 모서리전위의 K 보다 작다는 것을 발견했는데, 이는 나사 전위의 핵 생성이 모서리 전위보다 더 쉽다는 것을 의미한다. 최종적으로 나사전위와 모서리전위는 용질원자의 함량 0.05 at% 이상에서 V, Cr, Mn, Co이 우수할 것으로 보인다.
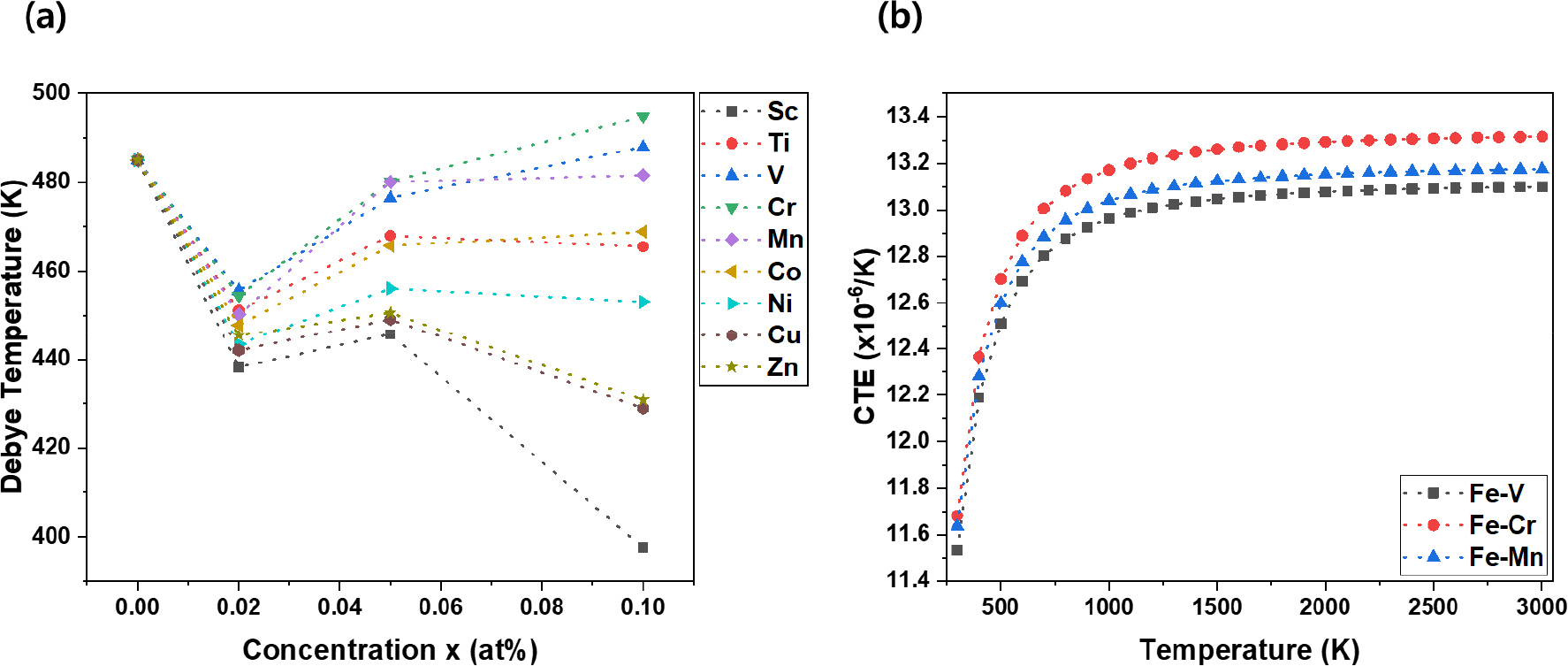
Fig. 7(a, b)는 첨가원소와 함량에 따른 Fe1-xMx 합금의 열팽창계수와 디바이온도(Debye temperature)를 나타내었다. 최종적으로 조성을 선별하기 전 디바이 온도를 이용하여 낮은 열전도도를 가지는 합금조성을 선별할 수 있었다. Fig. 7(a)의 디바이온도는 결정격자에서 포논이 균일하게 반복운동을 할 때 가장 높은 온도를 나타내는 지표이다.43) 디바이 온도가 높은 물질은 상온에서 포논 군집이 작기 때문에 평균자유경로를 결정하는 포논-포논 산란확률이 감소하기 때문에 열에 대한 저항이 작아진다.44,45) 모든 조성의 디바이온도는 용질원자 함량의 증가에 따라 α-Fe보다 감소하였다. 하지만, 0.1 at% 함량에서 Cr 용질원자가 포함되었을 경우 α-Fe보다 높은 것으로 관찰되었다. 그러므로 Cr 용질원자가 포함되었을 때 가장 낮은 열전도도를 가질 것으로 예상된다. 최종적으로 Sc, Ti, V, Cr, Mn, Co, Ni, Cu, Zn 원소 중 우수한 기계적 특성과 낮은 열전도도를 가지고 있는 V, Cr, Mn이 첨가된 합금을 선별하였다. 선별된 조성은 온도에 따른 열팽창계수를 비교 분석하였다. 특히, 선별된 조성들은 0.1 at% 함량 첨가되었을 때 가장 높은 기계적 특성을 보여주므로 3가지 조성을 조사하였다. Fig. 7(b)의 열팽창계수는 공통적으로 모든 조성에서 0~700 K까지 급격한 열팽창 변화를 보여주었다. 하지만, 각각의 조성별 열팽창계수 차이는 크지 않았다. Fe-Cr > Fe-Mn > Fe-V 순으로 작은 열팽창계수를 보여주었다.
4. 결 론
본 연구에서는 α-Fe계 이원계 저합금강의 격자상수, 탄성 상수에 대한 합금 효과는 제1원리계산을 사용하여 계산하였다. 합금 조성과 함량에 따른 형성에너지와 응집에너지를 비교한 결과 가장 안정한 합금은 Fe-Ti, Fe-V, Fe-Co, Fe-Ni라는 것을 알 수 있었다. 연성에 대한 합금 효과는 Poisson’s ratio 및 Pugh’s constant로 평가하였다. 순수한 α-Fe의 고유 연성이 Cr, Ni 용질원자에 따라 가장 많이 향상됨을 알 수 있다. 경도의 경우 V, Cr, Mn의 경우 일정수준 이상 첨가할 경우 내마모성을 강화될 것으로 예상된다. 또한, 경험식을 이용하여 합금의 나선전위 및 모서리전위의 경도와 에너지 계수를 조사하였다. 용질원자 함량이 0.05 at% 이상 증가할 경우 순수한 α-Fe보다 나사전위 및 모서리전위가 증가하는 것을 관찰하였다. 또한, Cr 용질원자가 0.1 at% 함량이 포함될 경우 저열전도도와 저열팽창을 가지는 합금을 형성할 수 있을 것으로 예상된다. 본 이론적 연구는 저합금강의 기계적 특성과 열팽창에 대한 용질 원자 효과를 제공하며, 이러한 합금의 조성 최적화를 위한 가이드를 제공할 수 있을 것이다.